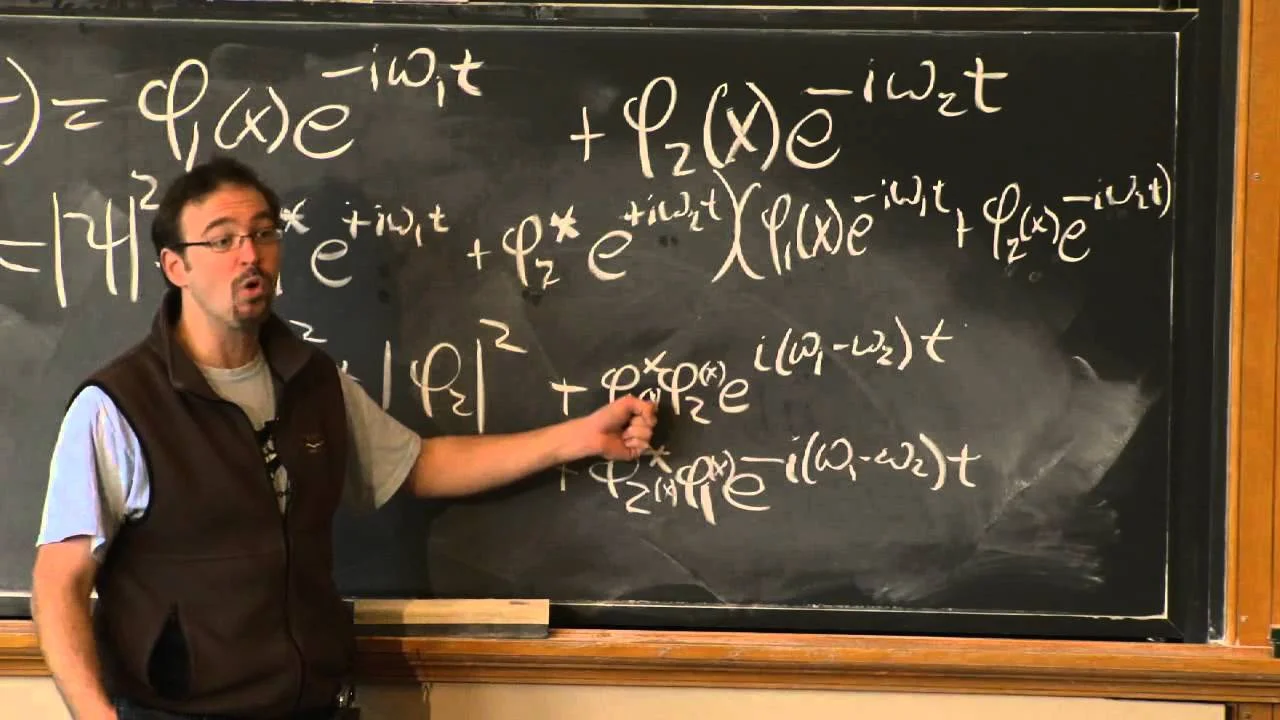In this lesson, we'll derive an equation which will allow us to calculate the wavefunction (which is to say, the collection of probability amplitudes) associated with any ket vector \(|\psi⟩\). Knowing the wavefunction is very important since we use probability amplitudes to calculate the probability of measuring eigenvalues (i.e. the position or momentum of a quantum system).
Schrodinger's Time-Dependent Equation: Time-Evolution of State Vectors
Newton's second law describes how the classical state {\(\vec{p_i}, \vec{R_i}\)} of a classical system changes with time based on the initial position and configuration \(\vec{R_i}\), and also the initial momentum \(\vec{p_i}\). We'll see that Schrodinger's equation is the quantum analogue of Newton's second law and describes the time-evolution of a quantum state \(|\psi(t)⟩\) based on the following two initial conditions: the energy and initial state of the system.
Overview of Single-Variable Calculus
In this lesson, we'll give a broad overview and description of single-variable calculus. Single-variable calculus is a big tool kit for finding the slope or area underneath any arbitrary function \(f(x)\) which is smooth and continuous. If the slope of \(f(x)\) is constant, then we don't need calculus to find the slope or area; but when the slope of \(f(x)\) is a variable, then we must use a tool called a derivative to find the slope and another tool called an integral to find the area.
PERIODIC WAVEFUNCTIONS HAVE QUANTIZED EIGENVALUES OF MOMENTA AND ANGULAR MOMENTA
The wavefunction \(\psi(L,t)\) is confined to a circle whenever the eigenvalues L of a particle are only nonzero on the points along a circle. When the wavefunction \(\psi(L,t)\) associated with a particle has non-zero values only on points along a circle of radius \(r\), the eigenvalues \(p\) (of the momentum operator \(\hat{P}\)) are quantized—they come in discrete multiples of \(n\frac{ℏ}{r}\) where \(n=1,2,…\) Since the eigenvalues for angular momentum are \(L=pr=nℏ\), it follows that angular momentum is also quantized.
The Eigenvectors of any Hermitian Operator must be Orthogonal
Origin of Structure and "Clumpyness"
In this lesson we'll explain why there is structure and "clumpyness" in the universe. In other words, why there is more stuff here than over there. Now, if all of the distribution of matter and energy in the universe was initially completely uniform (meaning homogenous and isotropic), then galaxies, stars, and people would have never formed. Non-uniform density would never arise in such a universe. But due to the time-energy uncertainty principle, the distribution of matter and energy must have had been randomly distributed throughout space at the beginning of the universe. Since the distribution was truly random, there would always be regions of space with slight more matter and energy than other. These slight non-uniformities ("imprinted" by the uncertainty principle) in matter and energy density throughout space near the beginning of the universe is the origin of the slight non-uniformities that we see in the CMBR.
How initial states of definite energy change with time
In general, if a quantum system starts out in any arbitrary state, it will evolve with time according to Schrödinger's equation such that the probability \(P(L)\) changes with time. In this lesson, we'll prove that if a quantum system starts out in an energy eigenstate, then the probability \(P(L)\) of measuring any physical quantity will not change with time.
Quantum Dynamics
CRISPR-CAS9 Gene Editing
Superconductors: the Future of Transportation and Electric Transmission
Superconductors are the key to unlocking the future of transportation and electrical transmission. They enable the most efficient approaches to these industrial processes known to present science. A maglev vehicle, to borrow Jeremy Rifkin's wording, will shrink the dimensions of space and time by allowing distant continental and inter-continental regions to be accessed in, well, not much time at all. But superconductors also offer unprecedented efficiency: they eliminate the problem of atoms colliding with other atoms and would allow vehicle to "slide" across enormous distances with virtually no loss of energy and it would allow a loop of current to persist longer than the remaining lifetime of the universe. Much of the damage accumulated in the components of vehicles can, in some way or another, be traced to the friction against the road; maglev transportation circumvents this issue.