In this section, we delve into some very fundamental ideas which, although expressed with respect to different quantities, are the basis of not only classical mechanics but also relativistic and quantum mechanics as well. These three areas of physics describe the universe within different ranges of parameters: quantum mechanics deals with things on the smallest scale; classical mechanics deals mostly with the size-range of macroscopic objects that we are all familiar with; and general relativity describes the most massive objects in the universe. All of these areas of physics involve some notion of inertia, a state which does not change; each of these areas also have an equation of motion which describes how inertial motion changes. We'll discover that the notions of inertial motion and the change in inertial motion can be expressed in terms of a very small number of elementary rules; and yet, these rules encapsulate a myriad of predictions which encompasses all observable phenomena within a given range of parameters.

The difference between kinematics, dynamics, and mechanics and what each of these terms means is a common point of confusion. But in the most basic sense, the meanings and differences of each of these terms can be described as follows: kinematics describes the motion of an object without consideration of what caused that motion; dynamics describes what caused that motion (namely, a force) without consideration of what the motion of the object is; and mechanics combines the two and describes both the motion and cause of the motion.

Many of the concepts we use in physics are very abstract and "non-visualizable." But, nonetheless, they can be applied to tell us a great deal about how the universe works. For example, the concepts of angular momentum and the conservation of angular momentum are very abstract and it might, at least initially, not seem to have much to do with anything based in physical reality—as Feynman probably would've said, the latter is just a number that we keep measuring to be the same. But when these concepts are applied, they actually "say" or predict a lot about how the universe works: this law requires everything from solar systems being flat to a spinning ice skater rotating faster as they bring their arms in.

Kinematics is the study of the position (represented by the position vector \(\vec{R}(t)\)) of an object as a function of time. The position vector can be used to define other quantities such as velocity \(\vec{v}\) and acceleration \(\vec{a}\); all three of these quantities, together, can fully describe the motion of any object. In this lesson, we'll study these three fundamental quantities of kinematics.

Galileo once pondered how one could describe the motion of cannonballs and other projectiles moving near Earth's surface. Since Aristotle, philosophers had tried for millennia to tackle this problem but it wasn't until Newton invented calculus and formulated the laws of classical mechanics when this question was finally answered. In this lesson, we'll use calculus and Newton's laws to answer this nearly 2,500 year old problem and derive the equations of motion governing projectile motion.

In this lesson, we'll discuss the foundation of Classical mechanics: namely, Newton's three laws of motion. Everything else that we discuss in Classical mechanics will be based on these principles.

Newton's law of gravity has been described as one of the greatest achievements in human thought of all time. It says that everything in the universe is, quite literally, connected. It must've been an astonishing realization to Newton that a grain of dust in his room exerts a slight "pull" on all of the stars and galaxies in the universe. In the words of Paul Dirac: "Pick a flower on Earth and you move the farthest star."

Using Newton's law of gravity and the concept of the definite integral, we can find the total gravitational force exerted by a rod on a particle a horizontal distance \(d\) away from the rod.

To find the gravitational force exerted by a disk on a particle a height \(h\) above the center of the disk, we must use Newton's law of gravity and the concept of a definite integral.

To find the gravitational force exerted by a sphere of mass \(M\) on a particle of mass \(m\) outside of that sphere, we must first subdivide that sphere into many very skinny shells and find the gravitational force exerted by anyone of those shells on \(m\). We'll see, however, that finding the gravitational force exerted by such a shell is in of itself a somewhat tedious exercise. In the end, we'll see that the gravitational force exerted by a sphere of mass \(M\) on a particle of mass \(m\) outside of the sphere (where \(D\) is the center-to-center separation distance between the sphere and the particle) is completely identical to the gravitational force exerted by a particle of mass \(M\) on the other particle of mass \(m\) such that \(D\) is there separation distance.
 

In this lesson, we'll analyze the motion of object's falling near the Earth's surface at slow velocities.

What is work? Work is a measure of how much total energy is transferred into or out of an object. In this lesson we'll see that by calculating the work done on an object (how much energy is transferred into or out of it), we can predict the object's future state of motion.

In this lesson, we'll discuss how the total work \(W\) on an object depends on the angle \(\theta\) at which the force \(\vec{F}\) is applied to the object.

Work is energy transfer. But what happens when work is done on an object such that its height above the ground doesn't change? The answer is that only kinetic energy is transferred into or out of the object. And since work is the total amount of energy transfered into or out of the object, it therefore follows that the work is just equal to the object's change in kinetic energy.

What happens if the only effect of the work done on an object is to change its height without changing its speed? The answer is that the work done on the object only changes in potential energy. In this lesson, we'll consider the work done by Earth's gravity on an object whose height above the ground changes but whose speed stays the same.

In this lesson, we'll introduce the notion of linear momentum. 

In this lesson, we'll show that the principle of momentum conservation can be derived using Newton's laws of motion.

In this lesson, we'll apply the principle of momentum conservation to analyze inelastic collisions which is when objects collide and "stick" together moving away as a single composite mass. We'll see that the conservation of momentum allows us to predict the motion after such a collision has occurred.

In this section, we discuss the various different kinds of mechanical waves: transverse, longitudinal, and some waves which have both of those aspects. Mechanical waves are disturbances which propagate through a medium and transport energy from one region of space to another. In this section, we'll start off with a qualitative description of what mechanical waves.

There are many different ways to describe rotational motion, but the most convenient way of doing so is to replace the role played by the position vector in linear motion with an angular coordinate. This will give us a way of describing the rotational motion of rigid bodies where we do not have to worry about the individual positions of every particle.

Rotational kinetic energy is not a new concept: it is just the sum of all the translational kinetic energies of all the particles comprising a system. Just like how translational kinetic energy is a very important concept in simplifying many problems related to linear motion, the same is true of rotational kinetic energy for rotational motion. Very often, in complicated situations, it is much simpler to use energy concepts than concepts related to force or torque.

We'll see that torque, rotational inertia and rotational acceleration play the same role in rotational mechanics as force, mass, and linear acceleration play in linear motion. Torque is, roughly speaking, how good of a job a given applied force will do at changing the, otherwise, uniform rotational motion; rotational inertia is how much an object resists having its rotational motion changed; and rotational acceleration captures how much the rotational motion is changing from its state of uniform rotational motion. In this section, we'll spend a lot of time focusing on developing a qualitative understanding of torque. We shall also quantify torque and end the section by deriving the rotational analogue of Newton's second law.

Everything in this section will summarize some—a fairly good portion—of what we'll be studying in much more detail in the subsequent sections.

In this section, we'll derive the Euler-Lagrange equation. The Euler-Lagrange equation is a differential equation whose solution minimizes some quantity which is a functional. There are many applications of this equation (such as the two in the subsequent sections) but perhaps the most fruitful one was generalizing Newton's second law. This equation, together with Hamilton's principle, allows us to generalize Newtonian mechanics and find the motion of systems using generalized coordinates—all of a sudden, double-pendulums don't seem so scary.

In this section, we'll find the solution (which is a curve x(y)) to the Euler-Lagrange equation where the quantity being minimized is the arc length between any two points on a cylinder. That might sound like a mouthful, but we'll see that hopefully it isn't too bad.

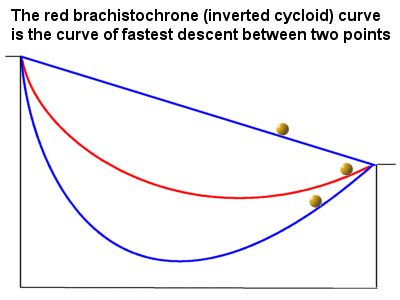
The Brachistochrone problem is a very famous problem in the history of physics and is as follows: find the path in which a particle under only the action of gravity will move from one point to another fastest and in the shortest amount of time possible.

In this lesson, we'll give a brief explanation of what generalized coordinates are. Up till this point, we got away with a very vague and imprecise definition. But for some of the problems that we'll look at later (such as the double-pendulum problem), the more technical definition we develop in this lesson will be very useful.

Noether's Theorem is one of the most profound theorems in all of science, let alone physics. It implies that the very fabric of space and time give rise to the laws of nature and lead the mathematician David Hilbert to independently discover the general theory of relativity, alongside Einstein. Noether's theorem, in simplest terms, is the statement that for every symmetry (what a symmetry is is something we'll get to in this lecture) there is an associated conservation law. Our goal in this lecture will be to prove that and show that various different conservation laws follow from an associated symmetry.