Since most of the mass in our home Milky Way galaxy is at its center we would expect, from Newton's law of gravity and second law, that the tangential velocity of each star in our galaxy would increase with increasing distance away from the Milky Way's center. But observations showed that, actually, the tangential velocity of each star is roughly constant. There were many hypotheses put forward around the time of this discovery which attempted to reconcile Newton's laws with experiment. But today, the prevailing explanation of why the tangential velocities of the stars in our galaxy is roughly constant is the theory that an invisible substance known as dark matter pervades the galaxy. Researchers speculate that this substance is comprised of particles which do not interact with light or radiation and are therefore invisible.
Cosmic Microwave Background Radiation
The mapping of the Cosmic Microwave Background Radiation (CMBR) was hailed by Stephen Hawking as one of the greatest achievements in 20th-century science because it gave us an image of our "baby universe" when it was very young. The CMBR proved, beyond a shadow of a doubt, that the Big Bang theory—a prediction of Einstein's general theory of relativity—is correct. Before the CMBR, many did not think of cosmology as a serious science since it lacked high-precision experiments and measurements like astronomy; many viewed cosmology as merely theoretical speculation that could never be confirmed by experiment. Many people view the mapping of the CMBR as the turning point when cosmology transitioned from being purely theoretical to a truly experimentally rigorous science.
Dark Energy
In this lesson we'll use the FRW equation to solve for the scaling factor \(a(t)\) in a universe dominated by vacuum energy or dark energy. We'll see that the scaling factor grows exponentially with time; this means that not only is the size of the universe getting bigger and bigger with time, but the rate at which it is doing so is increasing. In other words, the expansion of the universe is accelerating with time.
Finding the Capacitance of a Parallel-Plate Capacitor
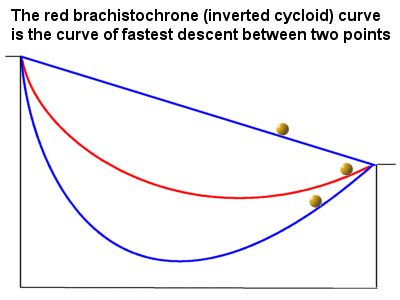
Brachistochrone problem
Generalized coordinates
In this lesson, we'll give a brief explanation of what generalized coordinates are. Up till this point, we got away with a very vague and imprecise definition. But for some of the problems that we'll look at later (such as the double-pendulum problem), the more technical definition we develop in this lesson will be very useful.
Finding the geodesic on a cylinder
Derivation of Guass's Law from Column's Law
Guass's law: for any charge distribution, whether a system of a finite number of point charges or a continuous distribution of charges, if I draw any arbitrary closed surface (which can be of any shape, size, and location), then the only contributions to the electric flux through that closed surface will be due to only the charges \(q_{enc}\) enclosed within that surface and that electric flux is given by the amount \(\frac{q_{enc}}{\epsilon_0}\). It is important to appreciate the word any to fully grasp the applicability of Guass's law: it applies to any closed surface and to any distribution of charge.
Introduction to Lagrangian Mechanics
Column's Law
Column's law describes the electric force between any distribution and number of charged particles. It is derived empirically and falls off inversely with the square of the distance, analogous to Newton's law of gravity. The practical usefulness of this law is that it allows one to determine the effect that any distribution of charge has on any other distribution of charge; this is analogous to how Newton's law of gravity allows one to determine the effects of one mass distribution on another. One very gradually learns this by solving many problems. But in this section, we'll start off with Column's law and then proceed to do some algebra and calculus in order to derive equations which describe the electric force that systems and continuous charge distributions exert on an individual particle.