Brachistochrone problem

This video was produced by The Kaizen Effect$^{[1]}$.

The brachistochrone problem is a very famous problem in the history of physics which was first solved by an excellent mathematician named Jean Bernoulli. He posed this problem as a challenge to the greatest mathematicians of Europe during the period of the Renaissance. He stated the problem as such:

We are given two fixed points in a vertical plane. A particle starts from rest at one of the points and travels to the other under its own weight. Find the path that the particle must follow in order to reach its destination in the briefest time.

In other words, if a particle's initial position is $(x_1,y_1)$ and it moves to a final position $(x_2,y_2)$ under only the action of gravity, the problem is to find the particular path $x(y)$ on the plane which, if the particle moved along that path, it would get to its final position fastest and in the least time. Like many problems in physics, this one involves idealizations of the physical system under consideration$^1$: in this problem, the object is approximated as a particle which is subjected only to the action of gravity. In all theoretical schemes in the past which were used to solve the brachistochrone problem, all of them necessarily had to obey fundamental laws such as the conservation of energy. The conservation of energy implies that (see below), no matter which path an object takes, the total velocity $v$ of the particle must be a function of height $y$ and of the form $v(y)=\sqrt{2gy}$. The change in the particle’s velocity depends on only its change in height.

$$\frac{1}{2}mv^2=mgy⇒v(y)=\sqrt{2gy}.$$

Bernoulli used a very sophisticated procedure to solve the brachistocrone problem. He new from Fermat's principle that it is a law of nature that light always moves along the path of least time and that light passes through materials of varying indices of refraction in accordance with Snell's law. He imagined stacking infinitely many, very thin sections of materials on top of each other where the refractive index varies smoothly from one layer to another. The velocity of a light beam passing through such a stack of materials, from Snell's law, would also vary smoothly as a function of height and can be written as $\vec{c}(y)$. This light beam would trace out a special path which is the path of least time for any object, not just light. This very creative way of thinking allowed Bernoulli to solve the brachistocrone problem.

But in this section, we'll use a much less sophisticated method to solve the brachistocrone problem than Bernoulli, Leibnez, Newton, and others. The goal of all the proceeding math of this section will be to express the quantity which we want to minimize (in this problem, the time $t$) as a functional which takes the form $S(q_j(x),q_j’(x),x)=t(x(y),x'(y),x)$. Then after that there will be a little more math, the goal of which will be to express the integrand as a functional of the form $F(q_j,q_j’,x)$. This will allow us to calculate all of the derivatives (in this problem, there are three of them) in the Euler-Lagrange equation; these simplifications will allow us to use the Euler-Lagrange equation (equations of motion) to solve for the path $x(y)$ which minimizes the functional (which is the time $t$).

Let's start out with our first goal of expressing the time as a functional. As the particle falls under the action of gravity, it's velocity is constantly changing. However, as the particle falls by a very, very small amount and traverses an infinitesimally small displacement $dS$, it's velocity is pretty much constant and we can write $dS=vdt$. Since we eventually want to be able to express the time as a functional, let's rearrange this equation in terms of time: $dt=\frac{dS}{v}$. Already, we have a rough idea of where we're trying to go with the math. First of all, we have a hunch that we'll probably have to take an integral since we want to express time as a functional of the form in Equation (3) from the section on the derivation of the Euler-Lagrange equation. So, let's do that:

$$\int_{t_1}^{t_2}dt=t=\int{\frac{dS}{v}}.\tag{1}$$

So we're one step closer to getting an equation which looks like Equation (3) from the derivation section, but the problem is that our integrand doesn't really look quite like the integrand in Equation (3). To achieve this goal of getting our integrand to look like the integrand in Equation (3), we'll need to express the velocity $v$ and the displacement $dS$ in terms of $x(y)$, $x'(y)$, and $y$. To achieve that goal for the velocity $v$, we can just use the conservation of energy as we did earlier to get $v(y)=\sqrt{2gy}$. So if we substitute this equation into Equation (1), we'll get

$$\int_{t_1}^{t_2}dt=t=\int{\frac{dS}{\sqrt{2gy}}};\tag{2}$$

and you can see that we have now expressed the time $t$ in terms of a $y$ term. Even before using the Pythagorean theorem to rewrite $dS$, by just going back to our derivation section (towards the beginning) you'll see that it will allow us to pick up a $x'(y)$ term. But that aside, from the Pythagorean theorem, we have $dS=\sqrt{1+\frac{dy}{dx}^2}dx$. If we substitute this into Equation (2), we get

$$t(x(y),x'(y),y)=∫\sqrt{1+\frac{dy}{dx}^2}(2gy)^{-1/2}dy=\frac{1}{\sqrt{2g}}\int{\sqrt{1+\biggl(\frac{dy}{dx}\biggl)^2y^{-1}}}dy.\tag{3}$$

So, you can see that both the time and the integrand in Equation (3) are functionals of the form we want. Thus, we can apply the analysis we used in our derivation to solve this problem. As a reminder—and I'm sure that by now this might seem like a broken record—the Euler-Lagrange equation is the condition which satisfies our functional being minimized. At this point, we basically just want to do a bunch of algebra to derive the motion $x(y)$ which satisfies the Euler-Lagrange equation—this will give us the path of least time. The first step to doing this will be to evaluate all of the derivatives in the Euler-Lagrange equation as shown in the video and below:

$$\frac{∂L}{∂x}=\frac{∂}{∂x}\biggl(\sqrt{1+\biggl(\frac{dx}{dy}\biggl)^2}\text{ }y^{-1/2}\biggl)=0$$

$$\frac{d}{dy}\frac{∂}{∂x'}\sqrt{\frac{1+\frac{dx}{dy}^2}{y}}=0.$$

Let's evaluate the partial derivative with respect to $x'$ to simplify the above equation to

$$\frac{d}{dy}\frac{(1+(x')^2)^{-1/2}}{\sqrt{y}}x'=0.$$

If the derivative of something is zero then that something must be constant and we get

$$\frac{(1+(x')^2)^{-1/2}}{\sqrt{y}}x'=C.$$

We shall let $C=\frac{1}{\sqrt{2a}}$ and we'll see later that the motivation for doing this is to be able make trigonometric substitutions to simplify our equation. By substituting for $C$ and doing some algebra, we get a series of simplifications as show in the video and below:

$$\frac{x'^2}{y(1+x'^2)}=\frac{1}{2a}$$

$$2ax'^2=y(1+x'^2)$$

$$(2a-y)x'^2=y$$

$$x'^2=\frac{y}{2a-y}$$

$$x'=\frac{y}{2a-y}.$$

Our goal this entire time has just been to isolate the solution $x(y)$, and we see that we are starting to get very close. All we have to do is "undo the derivative" on the left-hand side, so to speak, and we can do that by taking the anti-derivative, or the integral, on both sides of the equation:

$$x(y)=\int{\frac{y}{2a-y}}dy.$$

As intimidating as the integral above might look, solving it essentially just boils down to making a few trigonometric substitutions and a lot of algebra. If you are unfamiliar with the trigonometric substitutions used in the video above, I suggest refreshing your trigonometry skills by checking out the Khan Academy's videos on trigonometry. I'll omit the substitutions and algebra used to solve the integral since all of those steps are shown in the video; but after doing all the necessary trigonometry and algebra, what you end up with are the equations below:

$$x(θ)=a(θ-cosθ)$$

$$y(θ)=a(θ-sinθ)+C.$$

As described in the video above, the constant $C$ can be solved for by setting $x$ and $y$ equal to zero. Doing so, we find that $C=0$. The constant $a$ can also be solved for by substituting the appropriate conditions; but we won't worry about this and we'll just be concerned with what the graph of these parametric equations look like. The equations above simplify to

$$x(θ)=a(θ-cosθ)$$

$$y(θ)=a(θ-sinθ).$$

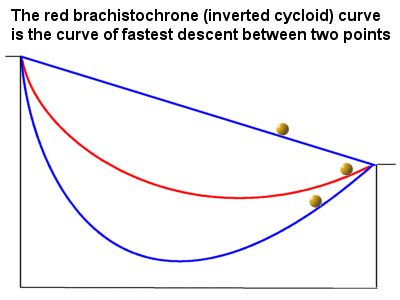
If we graph these equations, the curve we'll get is a cycloid. If a particle rolls down a frictionless (remember that we said the only force that can act on it is gravity) surface whose shape is that of a cycloid, it will fall from any arbitrary point along the surface to any other arbitrary point along the surface (at a lower height) in the least amount of time.

This article is licensed under a CC BY-NC-SA 4.0 license.

References

1. The Kaizen Effect. "Lagrangian Mechanics - Lesson 3: The Brachistochrone Problem". Online video clip. YouTube. YouTube, 21 May 2016. Web. 01 June 2016.

2. http://www.storyofmathematics.com/20th.html

3. Weisstein, Eric W. "Cycloid." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Cycloid.html

Notes

1. 1. It is always necessary that some combination of certain law, theories, approximations, and idealizations are assumed to be true in order for meaningful results to be mathematically deduced. The Euler-Lagrange equation is a mathematical deduction which is based upon the assumption that very fundamental laws are true. The fact that it is based on fundamental laws which are (or at least seem to be) universal and not approximations and theoretical schemes which are limited to very special circumstances means that the Euler-Lagrange equation is universal and applicable to nearly all situations (as long as these fundamental laws do not break down. One might think that the inapplicability of this equation to situations involving non-conservative forces limits their generality; while this is in fact the case in practice, it is not in principle since on the most fundamental level, there are no non-conservative forces in nature. For example, on the most fundamental level, friction (which is treated as non-conservative on macroscopic scales and in practice) is just the result of many atoms and molecules influencing each other via electromagnetic interactions (which are conservative forces).