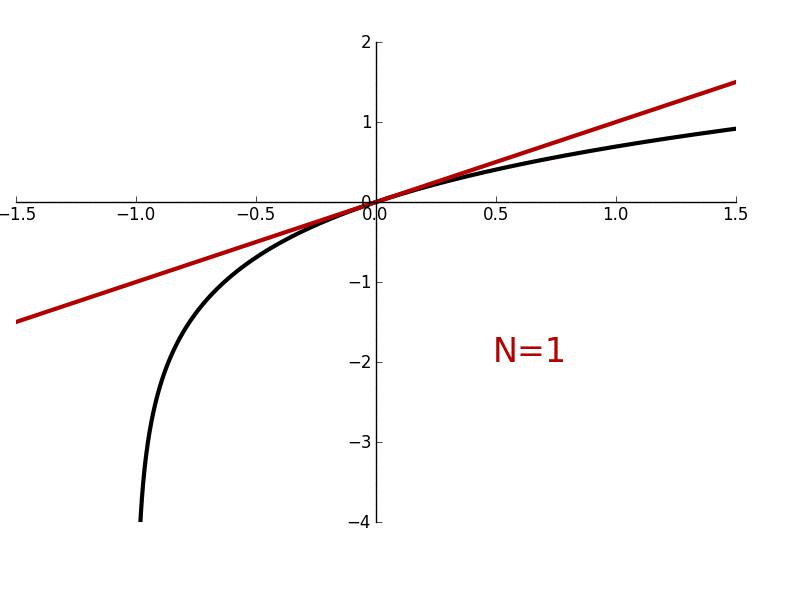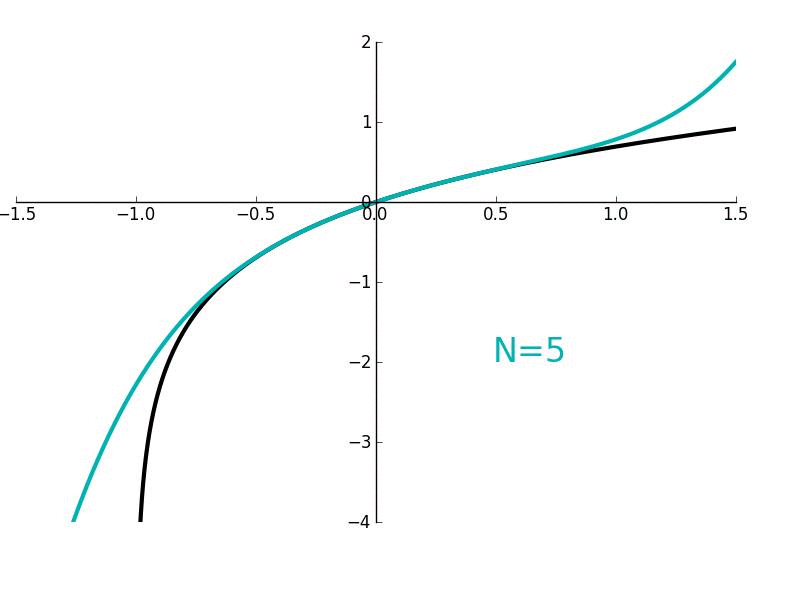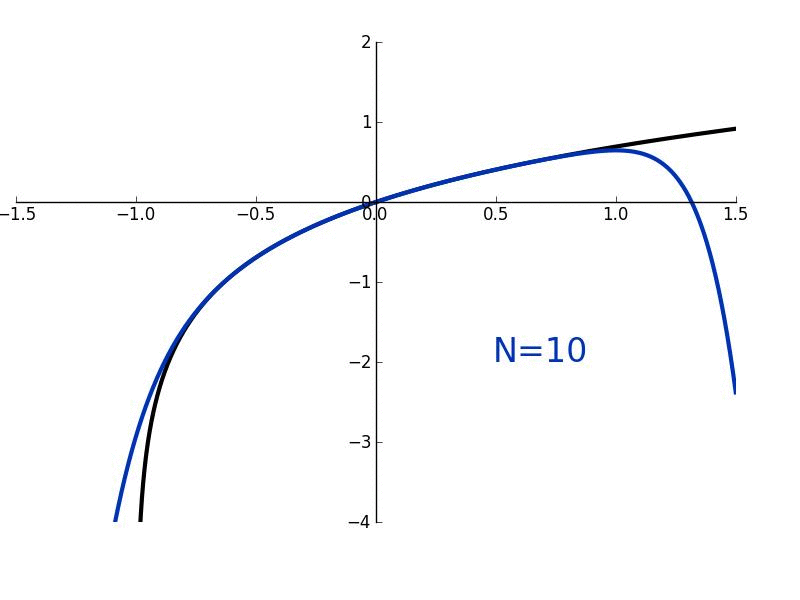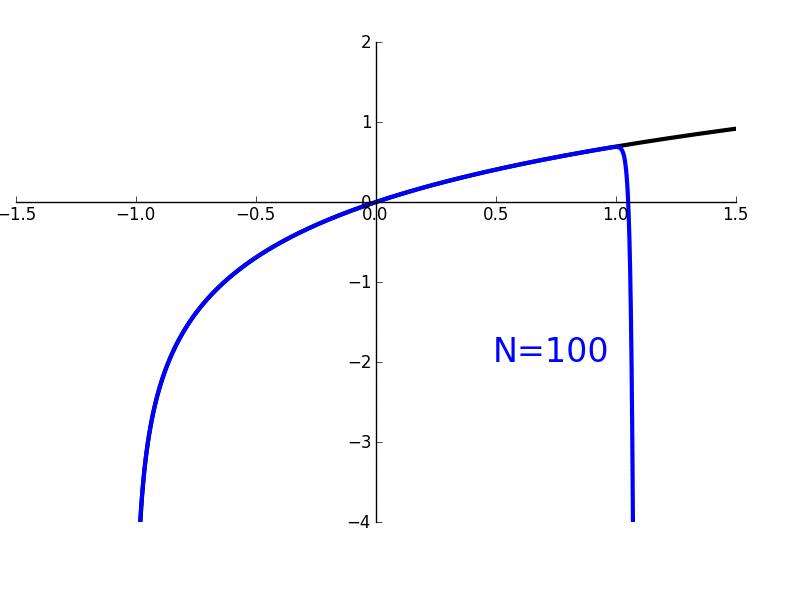In this lesson, we'll use the concept of a definite integral to calculate the volume of a sphere. First, we'll find the volume of a hemisphere by taking the infinite sum of infinitesimally skinny cylinders enclosed inside of the hemisphere. Then we'll multiply our answer by two and we'll be done.

In this lesson, we'll derive Maclaurin/Taylor polynomials which are used to "approximate" arbitrary functions which are smooth and continuous. More generally, they are used to give a local approximation of such functions. We'll also derive Maclaurin/Taylor series where the approximation becomes exact.

In this lesson, we define an integral as the Riemann sum as the number of rectangles approaches infinity.

Terraforming a world just means to make it more Earth-like. In this article, we'll discuss various techniques which have been proposed by scientists and engineers that would make Mars more like our home planet. We shall also discuss a potential scheme of future events which might occur as humans terraform and colonize Mars.

Time dilation is one of the many bizarre consequences of the speed of light being the same for everybody. For any observers in inertial frames of reference moving away from one another at a relative velocity which is close to that of the speed of light, they will see each others clocks run more slowly. In this section, we'll explore one of Einstein's original thought experiment: a train with a light clock moving past an observer standing idly at the train station. We'll see that the constancy of light speed with respect to all observers implies that time must slow down when watching events unfold in one frame of reference from another frame of reference if those two frames of reference are moving relative to each other. We'll start off by showing this for light beams bouncing off of two mirrors, but at the end we'll realize that this same argument applies to photons emitted between two atoms. The latter results in all physical clocks, chemical or biological, running more slowly.

In this section, we'll begin by seeing how Schrodinger's time-independent equation can be used to determine the wave function of a free particle. After that, we'll use Schrodinger's time-independent equation to solve for the allowed, quantized wave functions and allowed, energy eigenvalues of a "particle in a box"; this will be useful later on as a qualitative understanding of the quantized wave functions and energy eigenvalues of atoms.

In this lesson, we'll give a friendly introduction to what nuclear fusion is and how it might be used by space faring civilizations.

In this lesson we'll solve the FRW equation (one of the EFE's) for the scaling factor \(a(t)\) to determine the expansion rate of the universe in two different idealized scenarios: a universe filled with only radiation and a universe filled with only matter. These two different scenarios are called a radiation dominated universe and a matter dominated universe, respectively.

Shortly after Isaac Newton published his law of gravitation, the philosopher Richard Bentley and the astronomer Heinrich Olbers pointed out two paradoxes that arise from this law. The first, which is called Bentley's paradox, points out that if the universe is finite in size then, since the force of gravity is always attractive, all of the stars and galaxies in the universe should collapse in on themselves. The second, called Olbers' paradox, states that if the universe is infinite and if the distribution of stars in the universe is uniform then the night sky should be filled with infinitely many stars and the night sky should therefore be blindingly bright. 

Using Newton's law of gravity and shell theorem, we can derive the FRW equation. The FRW equation is a differential equation whose solution is the scaling factor \(a(t)\). The FRW equation essentially give us the relationship between the distribution of mass/energy and the scaling factor; we can use the FRW equation to find out what \(a(t)\) for various different kinds of mass/energy distributions including a universe dominated by matter, one dominated by radiation, or one dominated by vacuum energy. We'll see that the FRW equation predicts scenarios where the universe could be expanding. One might point out, and correctly so, that this contradicts Newton's law of gravity since, according to this law, gravity cannot act as a repulsive force. To reconcile this (and, we'll do this in a separate lesson), we could derive the FRW equation from Einstein's general theory of relativity by plugging the FRW metric into the Einstein Field Equations; plugging in the FRW metric, one could simplify the Einstein Field Equations to the FRW equation. This essentially would resolve the contradiction of the FRW equation predicting that, under the right circumstances, the universe could be expanding because general relativity (unlike Newton's law of gravity) allows for things like expanding universes.