Proper time
The proper time \(τ\) is the time measured by an observer \(O\) (which can just be a particle) who “stands still” in space relative to a coordinate system. For example, let's suppose that the origin of an \(x\), \(y\), \(z\) rectangular coordinate system is at a tree on Earth's surface. For convenience, we'll call this coordinate system the \(x^i\) coordinate system where \(i=1,2,3\) such that \(x^1\) represents the "\(x\) coordinate," \(x^2\) represents the "\(y\) coordinate," and \(x^3\) represents the "\(z\) coordinate." If I am standing still on the surface of the Earth one meter away from a tree (where I am standing still and not moving away from the tree) where the origin of a coordinate system \(x^i\) is located at the tree (and the coordinate system is fixed at that location), I will measure the proper time in this reference frame. Any other observer \(O'\) who is moving at a relative velocity away from the tree will measure some time \(t'\); according to the definition of proper time, they will not be measuring the proper time \(τ\).
Time Dilation
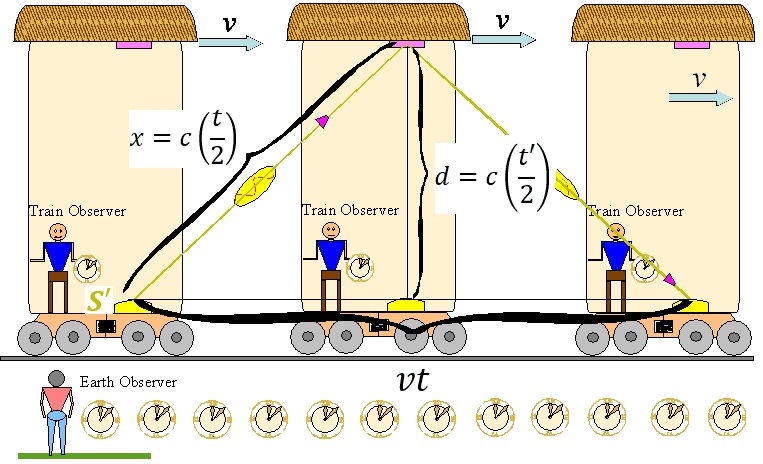
Figure 1: Right at the moment the train is passing by the observer standing at the train station, both observers clocks are synchronized; in other words, right at this moment, \(t=t'=0\). Also, right at this moment, a light source \(S'\) emits light in a direction towards a mirror (colored pink in image above) attached to the top of the train. The light beam eventually reaches the mirror and is reflected back towards \(S'\).
In one of Einstein’s original thought experiments, he imagined an observer \(O'\) riding in a train which was moving past another observer \(O\) standing still on the side of the tracks. The train was moving at a velocity of \(\vec{v}\) relative to \(O\). Two reference frames \(R'\) and \(R\) (which should be thought of as coordinate systems moving through space) are attached to \(O'\) and \(O\) respectively. The train is moving along only the \(x\)-axis in the \(R\)-frame; in the \(R'\)-frame no part of the train is moving through space along the \(x'\)-, \(y'\)- and \(z'\)-axes and is at rest. Right at the moment when \(O'\) is at \(x=0\) both observers clocks are synchronized and \(t'=t=0\). At this moment in time a light pulse is emitted from a light source \(S'\). This light pulse travels upwards along the vertical, bounces off of the mirror, and then arrives back at \(S'\). Let the distance between \(S'\) and the mirror be \(d\). In the \(R'\)-frame the light pulse travels along the \(y\)-axis at a constant speed \(c\). Let the time interval for the light pulse to travel from \(S'\) to the mirror and then back to \(S'\) (in the \(R'\)-frame) be \(Δt'\). Then the amount of time necessary for the light pulse to travel from \(S'\) to the mirror (the “half-way distance”) in the \(R'\)-frame is \(\frac{Δt'}{2}\). Since the speed of the light pulse is constant relative to \(R'\) then, from kinematics, we know that \(d=c\frac{Δt'}{2}\) and that
$$Δt'=\frac{2d}{c}.$$
We shall now see that the constancy of the speed of light with respect to both reference frames combined with the fact that the light pulse must travel through a greater distance with respect to the \(R\)-frame leads to \(O\) measuring a longer time interval \(Δt\) between event 1 (when the light pulse is emitted) and event 2 (when the light pulse arrives back at \(S'\)). If \(Δt\) is the time interval measured in the \(R\)-frame for the light pulse to travel from \(S'\) to the mirror and back to \(S'\), then the time interval measured in that frame for the light pulse to go from \(S'\) to the mirror is \(\frac{Δt}{2}\). By the time the light pulse reaches the mirror the train (and the mirror) will have moved a distance \(v\frac{Δt}{2}\) in the \(R\)-frame. Thus, in the \(R\)-frame, the light pulse must have traveled a horizontal distance \(v\frac{Δt}{2}\) and a vertical distance \(d\) in this time interval. Using the Pythagorean Theorem, the total distance the light pulse traveled is related to the horizontal and vertical distances by \(x^2=(v\frac{Δt}{2})^2+d^2\) where \(x\) is the total distance between \(S'\) and the mirror. The speed of light is a constant \(c=3×10^8\frac{m}{s}\) relative to \(R\) (as it is for any frame) and because this speed is constant it follows (from kinematics) that \(x=c\frac{Δt}{2}\) and \((c\frac{Δt}{2})^2=(v\frac{Δt}{2})^2+d^2\). If we solve for \(Δt\) we get
$$Δt=\frac{2d}{\sqrt{c^2-v^2}}=\frac{2d}{c\sqrt{1-\frac{v^2}{c^2}}}.$$
Since \(Δt'=\frac{2d}{c}\) we have
$$Δt=\frac{Δt'}{\sqrt{1-\frac{v^2}{c^2}}}.$$
Let's define a term called the Lorenz factor as being
$$γ≡\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}.\tag{1}$$
Figure 2: Using Equation (1), we can calculate the Lorenz factor for various different values of relative speed to obtain the graph above. As you can see, when the relative velocity between two reference frames is greater than 90% the speed of light, the effects of time dilation become enormous. Image by Zayani (Own work) [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0) or GFDL (http://www.gnu.org/copyleft/fdl.html)], via Wikimedia Commons
In the \(R'\)-frame events 1 and 2 occur at the same points in space (since there \((x'\text{ ,}y'\text{, }z')\) points are identical). Any observer who measures the time interval between two events in a frame in which those two events occur at the same points in space are said to be measuring the proper time interval \(Δτ\) between those two events. We see that \(Δt'=Δτ\) and that
$$Δt=γΔτ.\tag{2}$$
Because \(γ\) is always greater than one, it follows that \(Δt\) is always greater than \(Δτ\). Fundamentally, this means that whenever an observer is measuring the time interval between two events in a frame that are not at the same two spatial points, a time interval \(Δt\) will be measured that is always greater than \(Δτ\). The factor \(γ\) (which can be calculated using Equation (1)) represents how much longer \(Δt\) will be than \(Δτ\) based on the relative speed of both reference frames.
(It is important to mention that this effect only becomes important when \(γ\) significantly deviates from equaling one which only happens, roughly speaking, when \(v>0.01c\). When \(v>0.9c\), the Lorenz factor begins to blow up very rapidly.)
If \(O'\) started walking “carrying” his coordinate system (which is attached to him) around with him, he would be moving at a speed \(v\) relative to another frame corresponding to someone “standing still” on the train. If \(O'\) was carrying a clock, each tick would be occurring at the same coordinate point in the \(R'\)-frame and \(O'\) would therefore be measuring the proper time \(Δτ\); the person standing still on the train, however, would see each hand of the clock tick at a different coordinate point in his coordinate system and he would therefore be measuring the time \(Δt\). To the person standing still, the each hand of the clock would take a slightly longer time interval \(Δt\) to move from one position to another; to him, \(O'\)s clock would appear to be running a little slow. But since his walking speed is much slower than \(0.01c\), the effect of time dilation is negligible. Oftentimes, for practical purpose, if \(v<0.01c\), then we can assume that \(Δt=Δτ\). Only when \(v>0.01c\) does \(γ\) start to significantly deviate from being one.
On the most fundamental level, photons are emitted from atoms composing the light source \(S'\). Those photons then travel through space, bounce off the atoms composing the mirror, and arrive back at the atoms composing \(S'\). All chemical and biological processes are, at the most fundamental level, due to atoms interacting with other atoms via photons of light and electromagnetic radiation. The fact that it takes a longer time \(Δt\) for any two atoms to interact with one another via a photon of light/radiation going from one atom to another means that it takes longer for chemical, and therefore biological, interactions to occur. Therefore, \(O\) in the \(R\)-frame will see all physical processes on the train (indeed, a relativistic train going very fast) take a longer time to happen and the march of time for all events occuring on the train will progress more slowly in his reference frame.
This article is licensed under a CC BY-NC-SA 4.0 license.