Lesson overview
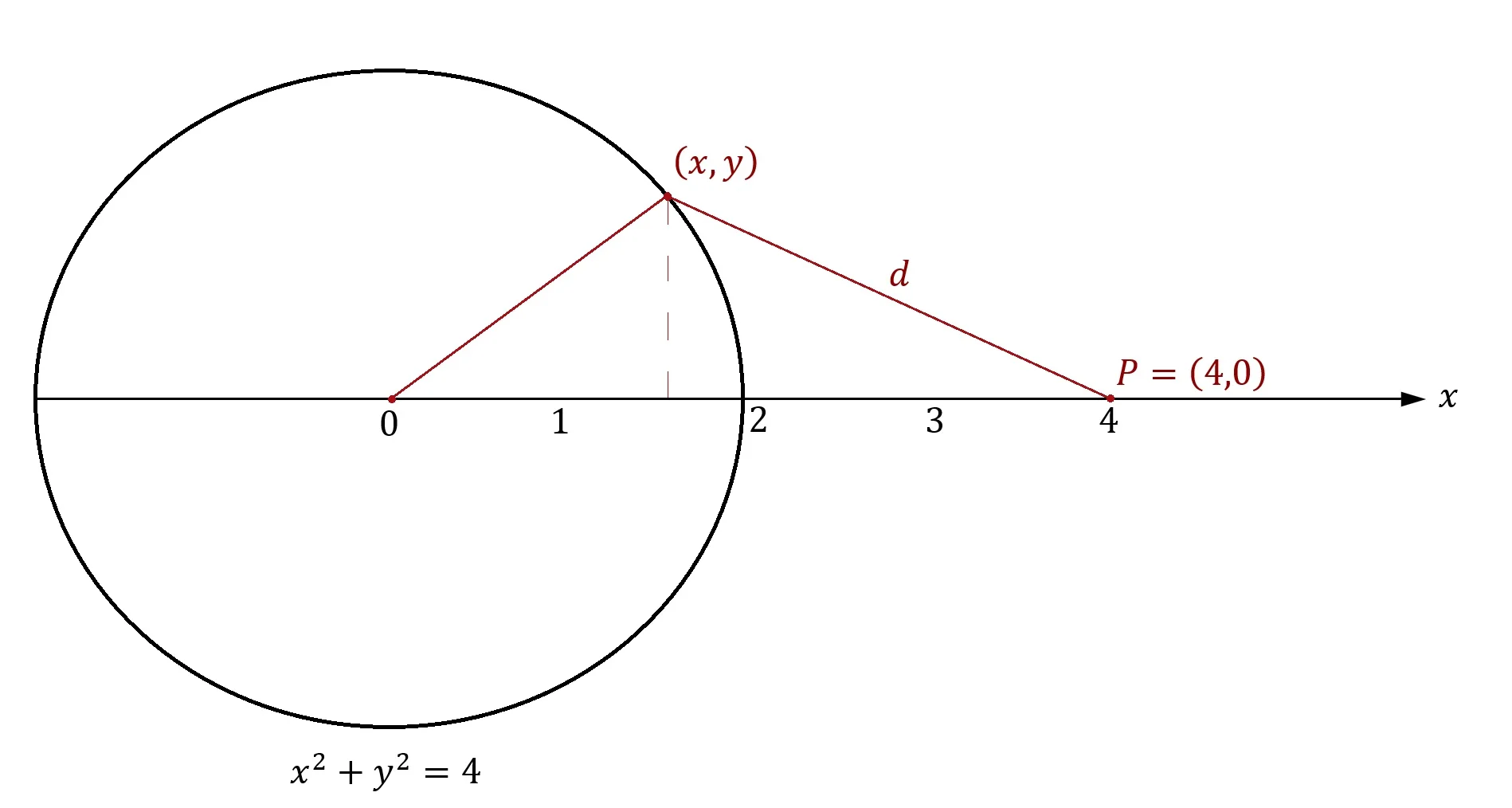
\(x^2+y^2=4\) centered at the origin of the \(x\)-axis, if\(P\) is the coordinate point \((4,0)\), and if \(d\) represents the distance between \((x,y)\) and \(P\) then, using only calculus, we can prove what point \((x,y)\) on the circle is associated with a minimum value of \(d\). Visually speaking, this problem is pretty obvious; clearly \(d\) is smallest when \((x,y)=(2,0)\). But in this lesson, we'll prove this statement using only calculus—more specifically, using only the calculus techniques we learned in the lesson, Finding the Minima and Maxima of a Function.
Finding the point \(\textbf{(x,y)}\) associated with the minimum distance between \(\textbf{(x,y)}\) and \(\textbf{P}\)
Figure 1: A graph of the circle \(x^2+y^2=4\) which is centered at the origin of the \(x\)-axis. If \((x,y)\) represents any point on the circle, if \(P\) is a point fixed at the coordinate point \((4,0)\), and if \(d\) represents the distance between those two points then, by using only calculus, we can find the point \((x,y)\) on the circle associated with the minimum distance \(d\).
In Figure 1, I have drawn a graph of a circle of radius \(r=2\) centered at the origin of an \(xy\)-plane. I have also drawn a point \(P\) at the coordinate point \((4,0)\). If we let \((x,y)\) be any point on the circle and if \(d\) is defined as the distance between the two points \((x,y)\) and \(P\), then our problem is to find the coordinate point \((x,y)\) on the circle for which the distance \(d\) is minimized by using the techniques we developed in previous lessons for finding the minima of a function. The solution to this problem is pretty obvious: clearly the point \((2,0)\) on the circle is associated with the minimum value of \(d\) which is given by \(d=2\). But let's determine the solution using only the calculus techniques we developed in previous lessons to check to see if these techniques actually work and lead to correct results.
We can see from Figure 1 that we can use the Pythagorean theorem to express \(d\) as
$$d=\sqrt{{x-4}^2+y^2}.\tag{1}$$
Since the equation of the circle in Figure 1 is given by \(x^2+y^2=4\), we can write
$$y^2=4-x^2.\tag{2}$$
Substituting Equation (2) into (1), we have
$$d=\sqrt{{x-4}^2+(4-x^2)}.\tag{3}$$
The reason why we went through the trouble of deriving Equation (2) is this: the calculus techniques of finding the minima of a quantity only apply to quantities expressed in the form of some function, \(f(x)\). Recall that these techniques allowed us to determine the value of \(x\) for which \(f(x)\). Recall that these techniques allowed us to determine the value of \(x\) for which \(f(x)\) was at a minimum value. With \(d\) now expressed as the function \(d(x)\) in Equation (4), we can use these techniques to find the value of \(x\) for which \(d\) is minimum. If we let \(s=d^2\), the value of \(x\) which minimizes \(d\) will also minimize \(s\). With that said, let's now focus on finding the minimum of \(s(x)\) given by
$$s=d^2=(x-4)^2+(4-x^2).\tag{4}$$
Taking the derivative of \(s\) with respect to \(x\), we have
$$s'(x)=2(x-4)·(1)+(-2)x.$$
and
$$s'(x)=2(x-4)-2x.\tag{5}$$
Setting the expression for \(s'(x)\) in Equation (6) equal to zero, we have
$$2(x-4)-2x=0.\tag{6}$$
If we increase the \(x\)-value in Equation (5) to a value slightly greater than \(x\) (associated with \(d'(x)=0\)), the function \(d'(x)\) increases and if we dcecrease the \(x\)-value in Equation (5) to a value slightly smaller than \(x\), \(d'(x)\) decreases. Thus, the \(x\) in Equation (6) must be associated with an \(x\)-value for which \(d'(x)\) is at a minimum. Solving for \(x\) in Equation (6), we have
$$-2x+8-2x=0$$
and
$$4x=8.$$
Thus,
$$x=2.$$
Using the equation of the circle in Figure 1, we can see that if \(x=2\), then
$$2^2+y^2=4$$
and
$$4+y^2=4.$$
Thus,
$$y=0.$$
Thus, using only the techniques of calculus, we have proved that the minimum distance \(d\) between the point \(P\) and any point \((x,y)\) on the circle \(x^2+y^2=4\) occurs at the point \((2,0)\).
This article is licensed under a CC BY-NC-SA 4.0 license.