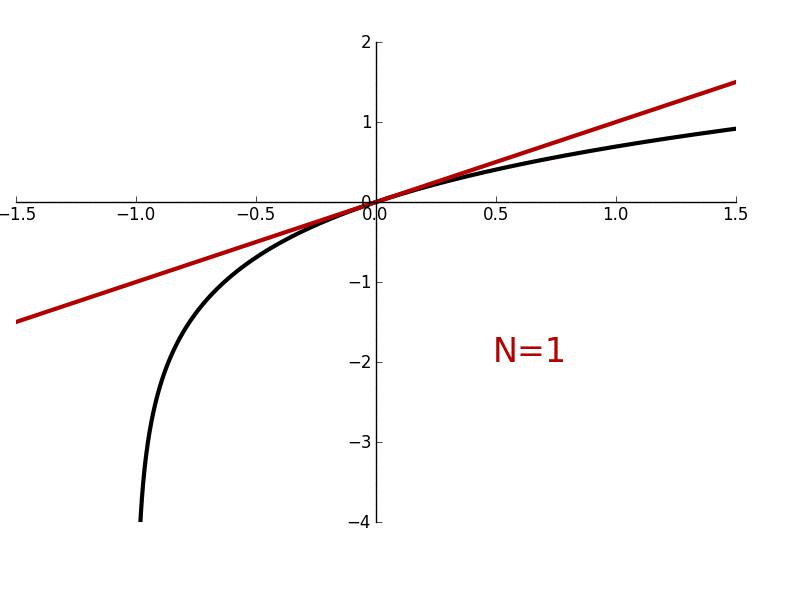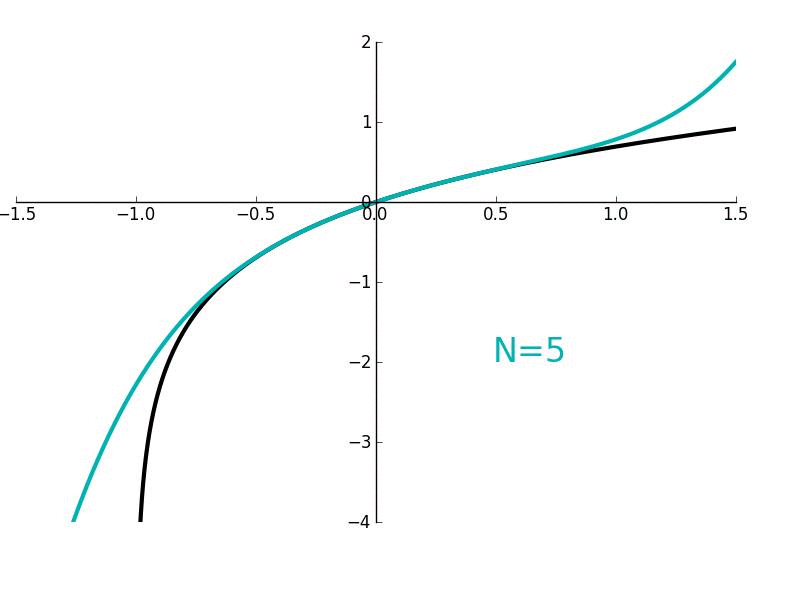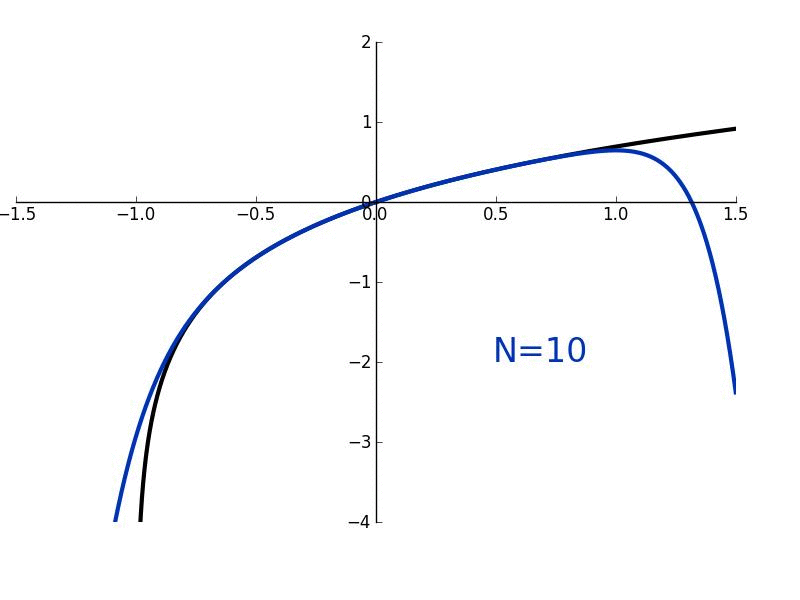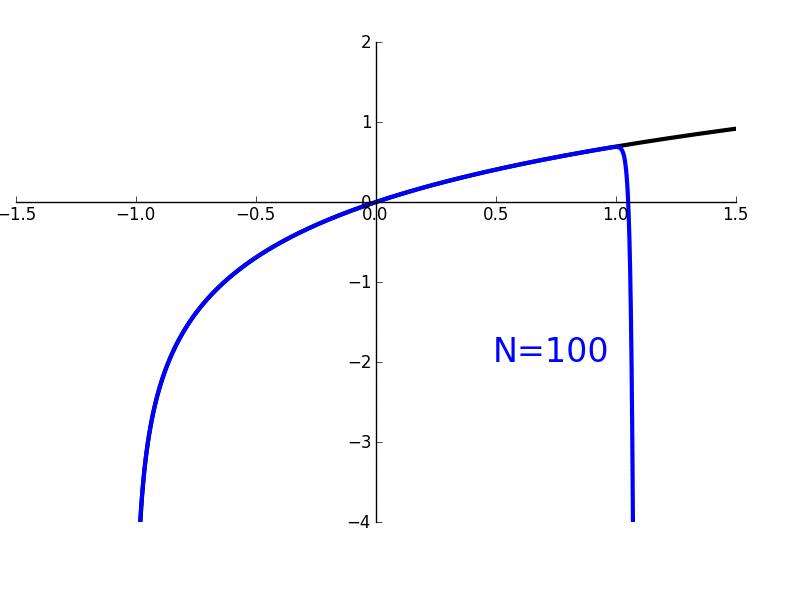Quantum Mechanics: Math Interlude

Complex numbers

Any ket vector \(|\psi⟩\) can be multiplied by a number \(z\) (which, in general can be real or complex) to produce a new vector \(|\phi⟩\):

$$z|\psi⟩=|\phi⟩.$$

In general, \(z=x+iy\). Sometimes the number \(z\) will just be a real number with no imaginary part, but in general it can have both a real and imaginary part. The complex conjugate of the number \(z\) is represented by \(z^*\) and is obtained by changing the sign of the imaginary part of \(z\); so \(z^*=x-iy\). Let’s look at some examples of complex numbers and their complex conjugates. Suppose that \(z\) is any real number with no imaginary part: \(z=x+(i·0)=x\). The complex conjugate of any real number is \(z^*=x-(i·0)=x\). In other words taking the complex conjugate \(z^*\) of any real number \(z=x\) just gives the real number back. Suppose, however, that \(z=x+iy\) is any complex number and we take the complex conjugate twice. Let’s see what we get. \(z^*\) is just \(z^*=x-iy\) (a new complex number). If we take the “complex conjugate of the complex conjugate,” we have \((z^*)^*=x+iy=z\). For any complex number \(z\),\(z^*=z\) .

If we multiply any complex number \(z\) by its complex conjugate \(z^*\), we’ll get

$$zz^*=(x=iy)(x-iy)=x^2-ixy+ixy-i^2y^2=x^2+y^2.$$

Figure 1: Any complex number \(z\) can be represented in either Cartesian coordinates as \(x+iy\) or in polar coordinates as \(re^{iθ}\).

For any complex number \(z\) the product \(z^*z\) is always a real number that is greater than or equal to zero. This product is called the modulus squared and, in a very rough sense, represents the length squared of a vector in a complex space. We can write the modulus squared as \(|z|^2=zz^*\). From Figure 1 we can also see that any complex number can be represented by \(z=x+iy=rcosθ+irsinθ=re^{iθ}\). The complex conjugate of this is \(z^*=x-iy=rcosθ+irsin(-θ)=re^{-iθ}\). The modulus squared of any vector in the complex plain is given by \(|z|^2=zz^*=(re^{iθ})(re^{iθ}=r^2\). If \(|z|^2=r^2=1\) and hence \(|z|=r=1\), then the magnitude of the complex vector is 1 and the vector is called normalized.

---

Column and row vectors and matrices

Any vector \(|A⟩\) can be expressed as a column vector: \(\begin{bmatrix}A_1 \\⋮ \\A_N\end{bmatrix}\). To multiply \(|A⟩\) by any number \(z\) we simply multiply each of the components of the column vector by \(z\) to get \(z|A⟩=z\begin{bmatrix}A_1 \\⋮ \\A_N\end{bmatrix}=\begin{bmatrix}zA_1 \\⋮ \\zA_N\end{bmatrix}\). We can add two complex vectors \(|A⟩\) and \(|B⟩\) to get a new complex vector \(|C⟩\). Each of the new components of \(|C⟩\) is obtained by adding the components of \(|A⟩\) and \(|B⟩\) to get \(|A⟩+|B⟩=\begin{bmatrix}A_1 \\⋮ \\A_N\end{bmatrix}+\begin{bmatrix}B_1 \\⋮ \\B_N\end{bmatrix}=\begin{bmatrix}A_1+B_1 \\⋮ \\A_N+B_N\end{bmatrix}=|C⟩\). For every ket vector \(|A⟩=\begin{bmatrix}A_1 \\⋮ \\A_N\end{bmatrix}\) there is an associated bra vector which is the complex conjugate of \(|A⟩\) and is given by \(⟨A|=\begin{bmatrix}A_1^* &... &A_N^*\end{bmatrix}\). The inner product between any two vectors \(|A⟩\) and \(|B⟩\) is written as \(⟨B|A⟩\). The outer product between any two vectors \(|A⟩\) and \(|B⟩\) is written as \(|A⟩⟨B|\). The rule for taking the inner product between any two such vectors is

$$⟨B|A⟩=\begin{bmatrix}B_1^* &... &B_N^*\end{bmatrix}\begin{bmatrix}A_1 \\⋮ \\A_N\end{bmatrix}=B_1^*A_1\text{+ ... +}B_N^*A_N.$$

Whenever you take the inner product of a vector \(|A⟩\) with itself you get

$$⟨A|A⟩=\begin{bmatrix}A_1^* &... &A_N^*\end{bmatrix}\begin{bmatrix}A_1 \\⋮ \\A_N\end{bmatrix}=A_1^*A_1\text{+ ... +}A_N^*A_N.$$

We learned earlier that the product between any number \(z\) (which can be a real number but is in general a complex number) and its complex conjugate \(z^*\) (written as ) is always a real number that is greater than or equal to zero. This means that each of the terms \(A_i^*A_i\) is greater than or equal to zero and, therefore, will always equal a real number greater than or equal to zero.

Suppose we have some arbitrary matrix \(\textbf{M}\) whose elements are given by

$$\textbf{M}=\begin{bmatrix}m_{11} &... &m_{N1} \\⋮ &\ddots &⋮ \\m_{1N} &... &m_{NN}\end{bmatrix}.$$

To find the transpose of this matrix (written as \(\textbf{M}^T\)) we interchange the order of the two lower indices of each element. (Another way of thinking about it is that we “reflect” each element about the diagonal.) When we do this we get

$$\textbf{M}^T=\begin{bmatrix}m_{11} &... &m_{1N} \\⋮ &\ddots &⋮ \\m_{N1} &... &m_{NN}\end{bmatrix}.$$

The Hermitian conjugate of a matrix (represented by \(\textbf{M}^†\)) is obtained by first taking the transpose of the matrix and then taking the complex conjugate of each element to get

$$\textbf{M}^†=\begin{bmatrix}m_{11}^* &... &m_{1N^*} \\⋮ &\ddots &⋮ \\m_{N1}^* &... &m_{NN}^*\end{bmatrix}.$$

We represent observables/measurable as linear Hermitian operators. In our electron spin example, the observable/measurable is given by the linear Hermitian operator \(\hat{σ}_r\).

---

This article is licensed under a CC BY-NC-SA 4.0 license.

---

Quantum Dynamics

In many situations, during the time interval in between a particle's initial and final states, the force acting on that particle can vary with time in a very complicated way where the details of the force over that time interval are unknown. The concept of energy enables us to think about systems which have very complicated forces acting on them. A particle could have a force acting on it described by a very general force function \(\vec{F}(\vec{r}.t)\); but by thinking about the energy of that particle we can understand the effects \(\vec{F}(\vec{r}.t)\) has on it. 

In Newtonian mechanics, for any force function \(\vec{F}(\vec{r}.t)\), the force is related to potential energy according to the equations

$$F(x)=\frac{-∂V(x)}{∂x}$$

$$F(y)=\frac{-∂V(y)}{∂y}$$

$$F(z)=\frac{-∂V(z)}{∂z}.\tag{1}$$

We can express Equations (1) in terms of Newton's second law:

$$\frac{-∂V(x)}{∂x}=\frac{∂p_x}{∂t}$$

$$\frac{-∂V(y)}{∂y}=\frac{∂p_y}{∂t}$$

$$\frac{-∂V(z)}{∂z}=\frac{∂p_z}{∂t}.\tag{2}$$

Equations (2) represent the laws of dynamics governing any particle with potential energy \(V(\vec{r})\) due to the force \(\vec{F}(\vec{r})\).

According to De Broglie's equation \(p=\frac{h}{𝜆}\), the bigger the momentum of an object the smaller the wavelength of the wavefunction. Particles which are very massive have a lot of momentum and the wavefunction \(\psi(x,t)\) associated with them has a very small wavelength—meaning it is an extremely localized wavepacket with very little uncertainty involved in measuring the position \(x\) of the particle. If the potential energy \(V(x)\) of the particle does not vary that much with respect to the size of the wavepacket, although it will flatten out over time it won't flatten out that much (especially for a very massive particle). Therefore, for a very massive particle with a very localized wavefunction where \(V(x)\) varies smoothly, \(<X> ≈ x\). Since \(<X> ≈ x\), there will be very little uncertainty in the computation \(\frac{-dV(x)}{dx}\) and \(-<\frac{dv}{dx}>≈ \frac{-dv}{dx}\). For very massive particles with highly localized wavefunction which aren't disturbed (by interacting with their environment via forces), Newton's second law is a good approximation of the dynamics governing their motion. 

When a particle is hit by a photon (which happens during any measurement) or an atom, its potential energy function \(V(x)\) spikes. This causes the wavefunction to become very dispersed; when this happens there is a tremondous amount of uncertainty in measuring the position of the particle. Thus \(\frac{d<X>}{dt}\) becomes big during the interaction and \(<P>\) changes. After the interaction, \(<P>\) will remain roughly constant. Much of quantum dynamics can be understood from how \(\psi(x,t)\) is effected by \(V(x)\).

The Eigenvalues of any Observable \(\hat{L}\) must be Real

An eigenvector of any operator \(\hat{M}\) is defined as simply a special particular vector \(|λ_M⟩\) such that the only effect of \(\hat{M}\) acting on \(|λ_M⟩\) is to span the vector by some constant \(λ_M\) (called the eigenvalue of \(\hat{M}\)). Any eigenvector \(|λ_M⟩\) and eigenvalue \(λ_M\) of \(\hat{M}\) is defined as

$$\hat{M}|λ_M⟩=λ_M|λ_M⟩.$$

Thus the eigenvectors and eigenvalues of any observable \(\hat{L}\) is defined as

$$\hat{L}|L⟩=L|L⟩.\tag{9}$$

Let’s take the Hermitian conjugate of both sides of Equation (9) to get

$$⟨L|\hat{L}^†=⟨L|L^*.\tag{10}$$

According to Principle 1, any observable \(\hat{L}\) is Hermitian. Since any Hermitian operator \(\hat{H}\) satisfies the equation \(\hat{H}=\(\hat{H}^†\), it follows that \(\hat{L}=\hat{L}^†\) and we can rewrite Equation (10) as

$$⟨L|\hat{L}=⟨L|L^*.\tag{11}$$

Let’s multiply both sides of Equation (9) by the bra \(⟨L|\) and both sides of equation (11) by the ket \(|L⟩\) to get

$$⟨L|\hat{L}|L⟩=L⟨L|L⟩\tag{12}$$

and

$$⟨L|\hat{L}|L⟩=L^*⟨L|L⟩.\tag{13}$$

Subtracting Equation (12) from Equation (13), we get

$$⟨L|\hat{L}|L⟩-⟨L|\hat{L}|L⟩=0=(L^*-L)⟨L|L⟩.\tag{14}$$

In general, \(⟨L|L⟩≠0\) and is equal to a number \(z\). Therefore it follows that, in general, \(L^*-L=0\) and \(L^*=L\). In order for a number \(z\) to equal its own complex conjugate, it must be real with no imaginary part. Thus, in general, the eigenvalue \(L\) of any observable \(\hat{L}\) is always real. This is a good thing; otherwise Principle 3 wouldn’t make any sense. Recall that principle 3 states that the possible measured values of any quantity (i.e. charge, position, electric field, etc.) are the eigenvalues \(L\) of the corresponding observable \(\hat{L}\). But the measured values obtained from an experiment are always real; in order for Principle 3 to be consistent with this fact, the eigenvalues \(L\) better be real too.

Pauli Matrices

The quantity \(\hat{σ}_n\) is called the 3-vector spin operator (or just spin operatory for short). This quantity can be represented as a 2x2 matrix as \(\hat{σ}_z=\begin{bmatrix}(σ_n)_{11} & (σ_n)_{12}\\(σ_n)_{21} & (σ_n)_{22}\end{bmatrix}\). The value of  \(\hat{σ}_n\)(that is to say, the value of each one of its entries) depends on the direction \(\vec{n}\) that \(A\) is oriented along; in other words, it depends on which component of spin \(\hat{σ}_n\) we’re measuring using \(A\). In order to measure a component of spin \(\hat{σ}_m\) in a different direction (say the \(\vec{m}\) direction) the apparatus \(A\) must be rotated; similarly the spin operator must also be “rotated” (mathematically) and, in general, \(\hat{σ}_m≠\hat{σ}_m\) and the values of their entries will be different.

We’ll start out by finding the values of the entries of \(\hat{σ}_z\)—the spin operator associated with the positive z-direction. The states \(|u⟩\) and \(|d⟩\) are eigenvectors of \(\hat{σ}_z\) with eigenvalues \(λ_u=σ_{z,u}=+1\) and \(λ_d=σ_{z,d}=-1\); or, written mathematically,

$$\hat{σ}_z|u⟩=σ_{z,u}|u⟩=|u⟩$$

$$\hat{σ}_z|d⟩=σ_{z,d}|d⟩=-|d⟩.\tag{15}$$

Recall that any ket vector can be represented as a column vector; in particular the eigenstates can be represented as \(|u⟩=\begin{bmatrix}1 \\0\end{bmatrix}\) and \(|d⟩=\begin{bmatrix}0 \\1\end{bmatrix}\). We can rewrite Equations (15) as

$$\begin{bmatrix}(σ_z)_{11} & (σ_z)_{12}\\(σ_z)_{21} & (σ_z)_{22}\end{bmatrix}\begin{bmatrix}1 \\0\end{bmatrix}=\begin{bmatrix}1 \\0\end{bmatrix}$$

$$\begin{bmatrix}(σ_z)_{11} & (σ_z)_{12}\\(σ_z)_{21} & (σ_z)_{22}\end{bmatrix}\begin{bmatrix}0 \\1\end{bmatrix}=-\begin{bmatrix}0 \\1\end{bmatrix}.\tag{16}$$

Using the first equation of Equations (16) we have

$$(σ_z)_{11}+(σ_z)_{12}·0=1⇒(σ_z)_{11}=1$$

and

$$(σ_z)_{21}+(σ_z)_{22}·0=0⇒(σ_z)_{21}=0.$$

Using the second equation from Equations (16) we have

$$(σ_z)_{11}·0+(σ_z)_{12}=1⇒(σ_z)_{12}=0$$

and

$$(σ_z)_{21}·0+(σ_z)_{22}=0⇒(σ_z)_{22}=-1.$$

Therefore,

$$\hat{σ}_z=\begin{bmatrix}1 & 0\\0 & -1\end{bmatrix}.\tag{17}$$

To derive the spin operator \(\hat{σ}_x\) we’ll go through a similar procedure. The eigenvectors of \(\hat{σ}_x\) are \(|r⟩\) and \(|l⟩\) with eigenvalues \(λ_r=σ_{x,r}=+1\) and \(λ_l=σ_{x,l}=-1\):

$$\hat{σ}_x|r⟩=σ_{x,r}|r⟩=|r⟩$$

$$\hat{σ}_x|l⟩=σ_{x,l}|l⟩=-|l⟩.\tag{18}$$

The states \(|r⟩\) and \(|l⟩\) can be written as linear superpositions of \(|u⟩\) and \(|d⟩\) as

$$|r⟩=\frac{1}{\sqrt{2}}|u⟩+\frac{1}{\sqrt{2}}|d⟩$$

$$|l⟩=\frac{1}{\sqrt{2}}|u⟩-\frac{1}{\sqrt{2}}|d⟩.\tag{19}$$

Substituting \(|u⟩=\begin{bmatrix}1 \\0\end{bmatrix}\) and \(|d⟩=\begin{bmatrix}0 \\1\end{bmatrix}\) we get

$$|r⟩=\begin{bmatrix}\frac{1}{\sqrt{2}} \\0\end{bmatrix}+\begin{bmatrix}0 \\\frac{1}{\sqrt{2}}\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}} \\\frac{1}{\sqrt{2}}\end{bmatrix}$$

$$|l⟩=\begin{bmatrix}\frac{1}{\sqrt{2}} \\0\end{bmatrix}+\begin{bmatrix}0 \\-\frac{1}{\sqrt{2}}\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}} \\-\frac{1}{\sqrt{2}}\end{bmatrix}.$$

We can rewrite Equations (19) in matrix form as

$$\begin{bmatrix}(σ_x)_{11} & (σ_x)_{12}\\(σ_x)_{21} & (σ_x)_{22}\end{bmatrix}\begin{bmatrix}\frac{1}{\sqrt{2}} \\\frac{1}{\sqrt{2}}\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}} \\\frac{1}{\sqrt{2}}\end{bmatrix}$$

$$\begin{bmatrix}(σ_x)_{11} & (σ_x)_{12}\\(σ_x)_{21} & (σ_x)_{22}\end{bmatrix}\begin{bmatrix}\frac{1}{\sqrt{2}} \\-\frac{1}{\sqrt{2}}\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}} \\-\frac{1}{\sqrt{2}}\end{bmatrix}.\tag{20}$$

By solving the four equation in Equations (20) we can find the values of each of the entries of \(\hat{σ}_x\) (just like we did for \(\hat{σ}_z\)) and obtain

$$\hat{σ}_x=\begin{bmatrix}0 & 1\\1 & 0\end{bmatrix}.\tag{21}$$

Lastly, we solve for \(hat{σ}_y\) the same exact way that we solved for \(hat{σ}_x\) to get

$$\hat{σ}_y=\begin{bmatrix}0 & -i\\i & 0\end{bmatrix}.\tag{22}$$

The three matrices associated with \(\hat{σ}_z\), \(\hat{σ}_x\), and \(\hat{σ}_y\) are called the Pauli matrices.

Fundamental Principles and Postulates of Quantum Mechanics

Principle 1: Whenever you measure any physical quantity \(L\), there is a Hermitian linear operator \(\hat{L}\) (called an observable) associated with that measurement.

Principle 2: Any arbitrary state of a quantum system is represented by a ket vector \(|\psi⟩\).

Principle 3: The possible measurable values of any quantity are the eigenvalues \(λ_L(=L)\) of \(\hat{L}\).

Principle 4: According to the Copenhagen interpretation of quantum mechanics, after measuring \(L\), the possible states a quantum system can end up in are the eigenvectors \(|λ_L⟩(=|L⟩\)) of \(\hat{L}\).

Principle 5: For any two states \(|\psi⟩\) and \(|\phi⟩\), the probability amplitude of the state changing from \(|\psi⟩\) to \(|\phi⟩\) is given by

$$\psi=⟨\phi|\psi⟩.\tag{1}$$

The probability \(P\) of the state changing from \(|\psi⟩\) and \(|\phi⟩\) can be calculated from the probability amplitude using the relationship

$$P=\psi^*\psi=⟨\psi|\phi⟩^*⟨\phi|\psi⟩=|\psi|^2.\tag{2}$$

From a purely mathematical point of view, any ket \(|\psi⟩\) in Hilbert space can be represented as a linear combination of basis vectors:

$$|\psi⟩=\sum_i{\psi_i|i⟩}.\tag{3}$$

The kets \(|1⟩\text{, ... ,}|n⟩\) represent any basis vectors and their coefficients \(\psi_1\text{, ... ,}\psi_n\) are, in general, complex numbers. We shall prove in the following sections that we can always find eigenvectors \(|L_1⟩\text{, ... ,}|L_n⟩\) of any observable \(\hat{L}\) that form a complete set of orthonormal basis vectors; therefore any state vector \(|\psi⟩\) can be represented as

\(|\psi⟩=\sum_i{\psi_i|L_i⟩}.\tag{4}\)

We’ll also prove that the collection of numbers \(\psi_i\) are given by

$$\psi_i=⟨L_i|\psi⟩\tag{5}$$

and represent the probability amplitude of a quantum system changing from the state \(|\psi⟩\) to one of the eigenstates \(|L_i⟩\) after a measurement of \(L\) is performed. The collection of all the probability amplitudes \(\psi_i\) is called the wavefunction. When the wavefunction \(\psi(L,t)\) associated with the state \(|\psi⟩\) becomes a continuous function of \(L\) (that is, the range of possible values of \(L\) becomes infinite and the number of probability amplitudes becomes infinite), we define \(|\psi|^2\) as the probability density. One example where \(\psi\) becomes continuous is for a particle which can have an infinite number of possible \(x\) positions. Then \(\psi\) becomes a continuous function of \(x\) (and, in general, also time \(t\)). Since \(|\psi(x,t)|^2\) is the probability density, the product \(|\psi(x,t)|^2dx\) is the probability of measuring \(L\) at the position \(x\) and at the time \(t\). The probability of measuring anything at the exact location \(x\) is in general zero. A far more useful question to ask is: what is the probability \(P(x+Δx,t)\) of measuring \(L\) within the range of x-values, \(x+Δx\)? This is given by the following equation:
$$P(x+Δx,t)=\int_{x}^{x+Δx} |\psi(x,t)|^2dx.\tag{6}$$
According to the normalization condition, the total probability of measuring \(L\) over all possible values of \(x\) must satisfy
$$P(x,t)=\int_{-∞}^{∞} |\psi(x,t)|^2dx=1.\tag{7}$$
If \(\psi(L,t)\) is continuous, then the inner product \(⟨\phi|\psi⟩\) is defined as
$$\psi(L,t)=⟨\phi|\psi⟩=\int_{-∞}^{∞} \phi^*{\psi}\text{ dL}.\tag{8}$$