Everything in this section will summarize some—a fairly good portion—of what we'll be studying in much more detail in the subsequent sections.

In this section, we'll derive the Euler-Lagrange equation. The Euler-Lagrange equation is a differential equation whose solution minimizes some quantity which is a functional. There are many applications of this equation (such as the two in the subsequent sections) but perhaps the most fruitful one was generalizing Newton's second law. This equation, together with Hamilton's principle, allows us to generalize Newtonian mechanics and find the motion of systems using generalized coordinates—all of a sudden, double-pendulums don't seem so scary.

In this section, we'll find the solution (which is a curve x(y)) to the Euler-Lagrange equation where the quantity being minimized is the arc length between any two points on a cylinder. That might sound like a mouthful, but we'll see that hopefully it isn't too bad.

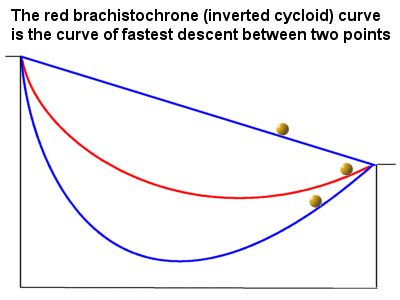
The Brachistochrone problem is a very famous problem in the history of physics and is as follows: find the path in which a particle under only the action of gravity will move from one point to another fastest and in the shortest amount of time possible.

In this lesson, we'll give a brief explanation of what generalized coordinates are. Up till this point, we got away with a very vague and imprecise definition. But for some of the problems that we'll look at later (such as the double-pendulum problem), the more technical definition we develop in this lesson will be very useful.

Noether's Theorem is one of the most profound theorems in all of science, let alone physics. It implies that the very fabric of space and time give rise to the laws of nature and lead the mathematician David Hilbert to independently discover the general theory of relativity, alongside Einstein. Noether's theorem, in simplest terms, is the statement that for every symmetry (what a symmetry is is something we'll get to in this lecture) there is an associated conservation law. Our goal in this lecture will be to prove that and show that various different conservation laws follow from an associated symmetry.