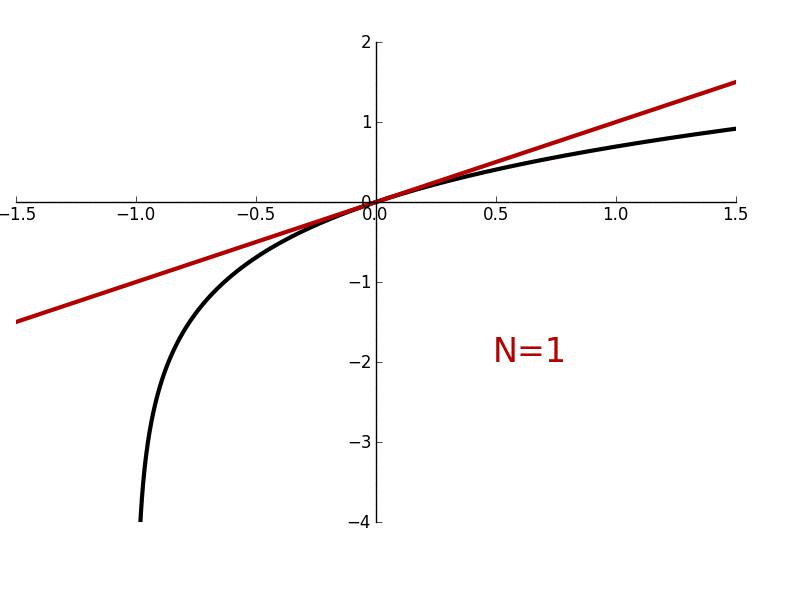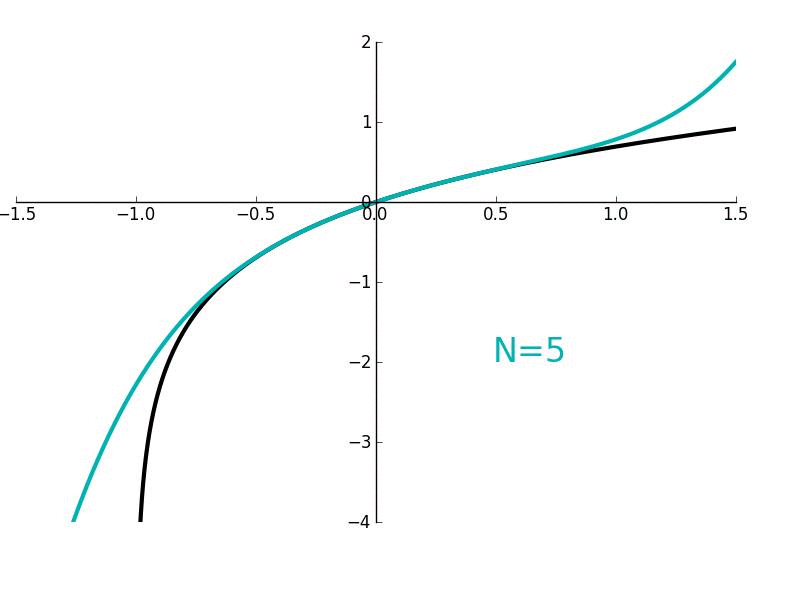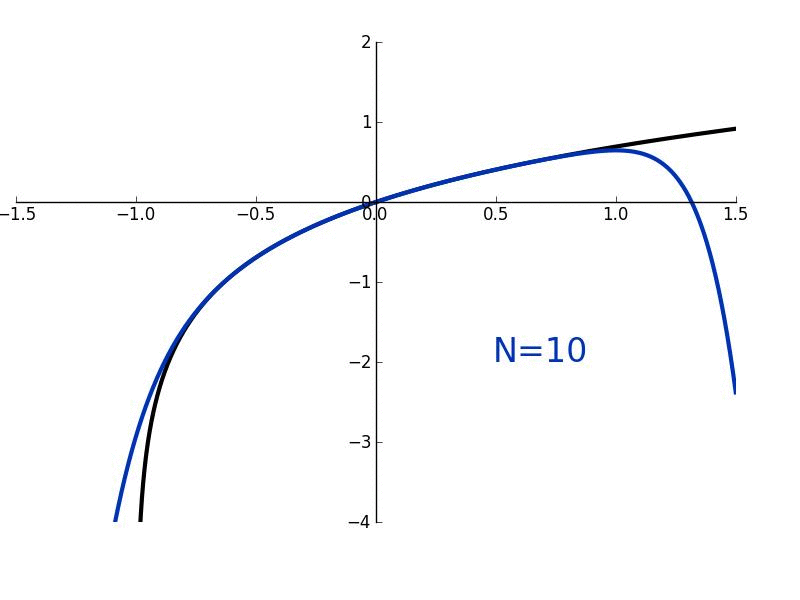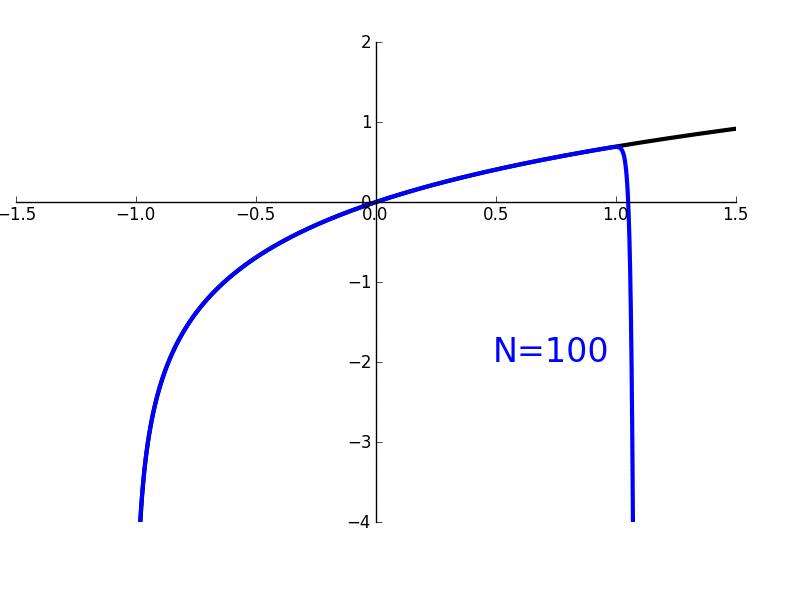Maclaurin polynomials and series
"Approximating a function at 0 using a polynomial." This video was produced by the Khan Academy.
In this lesson, we're going to focus on developing a technique for approximating the value of any arbitrary function \(f(x)\) at each value of \(x\) such that \(f(x)\) is smooth and continuous for all \(x\) values. How can we approximate \(f(x)\)? We'll approximate the value of \(f(x)\) with a function \(g(x)\) where the values of \(g(x)\) agree with the values of \(f(x)\) within a certain error \(E=|f(x)-g(x)|\). But the question is this: what kind of function would \(g(x)\) have to be to very closely "match" the values of \(f(x)\) at each value of \(x\)? It turns out that a polynomial function of the form
$$g(x)=c_0+c_1x+c_2x^2+...+c_nx^n,\tag{1}$$
would do the best job of approximating \(f(x)\). (At the moment, that claim might seem pretty ad hoc. But later, when we put \(f(x)\) and \(g(x)\) on the same graph, we'll see that Equation (1) is indeed a good approximation of any function \(f(x)\) that is smooth and continuous at every \(x\) value.) So let's say that we want \(g(x)\) to approximate \(f(x)\) at values of \(x\) close to \(x=0\). The first thing to notice here is that we can make our approximate function \(g(x)\) the same as the function \(f(x)\) (the function we want to approximate the best we can) by requiring that \(g(0)=f(0)\).
Let's now evaluate \(g(0)\) using Equation (1). If we substitute \(x=0\) into \(g(x)\), then Equation (1) simplifies to \(g(0)=c_0.\) Thus, we have shown that the first term in Equation (1) must be given by \(c_0=f(0).\) We are trying to "create" and "build" a function \(g(x)\) that is close to \(f(x)\); thus far we are at a good start since \(g(x)\) is identical to \(f(x)\) right at \(x=0\). But the problem is that as we move away from \(x=0\) to higher \(x\) values, \(g(0)=c_0\) is pretty far off. What we're going to show next is that by adding the additional term \(c_1x\) to \(c_0\), the expression \(c_0+c_1x\) will be a better approximate of \(f(x)\) (better than just \(c_0\), a pretty poor estimate away from \(x=0\)) for a bigger range of \(x\) values. To do this, let's start off by requiring that \(g'(0)=f'(0)\); that is to say, the derivative of the approximate function \(g(x)\) is the same as the function \(f(x)\) right at \(x=0\). To evaluate \(g'(x)\), let's start off by taking the derivative of \(g(x)\) (Equation (1)) to get
$$g'(x)=c_1+2c_2x+...+nc_nx^{n-1}.\tag{2}$$
Evaluating Equation (2) at \(x=0\), we have \(g'(0)=c_1\). Thus \(c_1=f'(0)\) and the second term in \(g(x)\) (see Equation (1)) must be given by \(f'(0)x\). Let's refer to the function \(f(0)+f'(0)x\) as \(g_1(x)\); then, \(g_1(x)=f(0)+f'(0)x\). Let's now graph \(g_1(x)\) in the same xy-plane as \(f(x)\) and see if it does a better job of estimating \(f(x)\) at more \(x\) values than \(c_0=f(0)\) (which we'll just called \(g_0(x)\)). In this example, we can see from Figure 1 that \(f(0)=0\); thus, \(g_1(x)\) must simplify to \(g_1(x)=f'(0)x\). We know from back in our days of algebra that the product of a slope (in this case, \(f'(0)\)) and a change in \(x\) (in this case, \(Δx=x-0\)) gives the value of a function at the point \(x\) such that that function is a straight line with a y-intercept of \(0\). Therefore, the function \(g_1(x)\) gives the y-value of each \(x\) along the straight red line (for \(n=1\)) in Figure 1. We can see from the graph in Figure 1 that \(g_1(x)\) is not only equal to \(f(x)\) at \(x=0\) like the function \(g_0(x)\), but since \(g_1(x)\) "hugs" \(f(x)\) more closely, it does a better job of approximating \(f(x)\) for more \(x\) values.
What we're going to show next is that by adding the third term \(c_2x^2\) to our approximate function, \(g_2(x)\) will "hug" \(f(x)\) even more closely as shown in Figure 1. But let's explain how we got to that graph of \(g_2(x)\) vs. \(x\) as shown in Figure 3. Let's require that \(g''(0)=f''(0)\). To find the expression for \(g''(0)\), let's start off by taking the derivative of both sides of Equation (2) to get:
$$g''(x)=2c_2+...+n(n-1)x^{n-2}.\tag{3}$$
Evaluating Equation (3) at \(x=0\), we see that \(g''(0)\) is given by \(g''(0)-2c_2\) and that \(\frac{g''(0)}{2}=c_2\). Thus, the third term in \(g(x)\) (Equation (1)) must be \(\frac{g''(0)}{2}x^2\). The expression for \(g_2(x)\) is given by
$$g_2(x)=f(0)+f'(0)x+\frac{f''(0)}{2}x^2.$$
Figure 1. Maclaurin polynomials of different order \(n\) (red curves) approximating the function \(e^x\) (blue curve).
Using MATLAB, we can find that the graph of \(g_2(x)\) vs. \(x\) is as shown in Figure 1. At first, when I was initially using the term "hugging," it might have been a little unclear what I meant by that. But hopefully, we can all understand what was meant by that term as we can see graphically that \(g_2(x)\) is "hugging" \(f(x)\) very closely within a certain range of \(x\) values. In fact, if you look at a pretty small range of \(x\) values around \(x=0\), it is pretty difficult to distinguish between \(f(x)\) and \(g_2(x)\). What if we wanted to derive the expressions for \(g_5(x)\), \(g_10(x)\), or \(g_n(x)=g(x)\)? How would we go about doing that? Well, it would essentially be analogous to how we got the expressions for \(g_0(x)\), \(g_1(x)\) and \(g_2(x)\). We would just have to take the derivative of \(g(x)\) a five, ten, or \(n\) number of times; then evaluate \(g(0)\), do some algebra, and then make a substitution to find either the fifth, tenth, or \(n\)th term in Equation (1). But let's skip some of those intermediate steps of finding the fourth through \((n-1)\)th terms and solve for the \(n\)th term in Equation (1). This will give us a general expression for our approximate function \(g(x)\). Taking the \(n\)th derivative of \(g(x)\) (represented as \(g^{(n)}(x)\)), we have
$$g^{(n)}(x)=n(n-1)(n-2)...·2·1·c_n.$$
Evaluating \(g^{(n)}(x)\) at \(x=0\) simply just gives us
$$g^{(n)}(0)=n(n-1)(n-2)...·2·1·c_n.$$
Analogous to all of the previous steps, we'll require that \(f^{(n)}(x)=g^{(n)}(x)\). Thus, the \(n\)th term of \(g(x)\) is given by
$$\frac{f^{(n)}(0)}{n(n-1)(n-2)...·2·1}x^n.$$
Using factorial notation, we can rewrite the term above simply as
$$\frac{f^{(n)}(x)}{n!}x^n.$$
If we substitute the first through \(n\)th terms of \(g(x)\) that we derived, Equation (1) simplifies to
$$g_n(x)=f(0)+f'(0)x+\frac{f''(0)}{2}x^2+...+\frac{f^{(n)}(x)}{n!}x^n.\tag{4}$$
Using Walfram Alpha, we can graph \(g_n(x)vs.x\) for all the different values of \(n\) as shown in Figure 1. The equation above is called an \(n\)th order Maclaurin polynomial and can be used to approximate any arbitary function \(f(x)\) so long as \(f(x)\) is smooth and continuous. Notice that the more number of terms \(n\) that we use in our approximation \(g_n(x)\), the better that the approximation is. Furthermore, as the number of terms \(n\) approaches infinity, the approximation becomes exact. Let's take the limit of both sides of the equation above as \(n→∞\):
$$\lim_{n→∞}g_n(x)=f(0)+f'(0)x+\frac{f''(0)}{2}x^2+...+\frac{f^{(n)}(0)}{n!}x^n+....\tag{4}$$
We can rewrite Equation (4) more compactly by using summation notation to get
$$\lim_{n→∞}g_n(x)=\lim_{n→∞}\sum_{i=0}^n\frac{f^{(n)}(0)x^n}{n!}.\tag{5}$$
Let's define the quantity \(g(x)\) as \(g(x)≡ \lim_{n→∞}g_n(x)\) simplifying Equation (5) to
$$g(x)=\lim_{n→∞}\sum_{i=0}^n\frac{f^{(n)}(0)x^n}{n!}.\tag{6}$$
As mentioned earlier, as the number of terms in the approximation becomes infinite, \(g(x)\) becomes equal to \(f(x)\). Equation (6) is called the Maclaurin series.
This article is licensed under a CC BY-NC-SA 4.0 license.
Sources: Khan Academy, Wikipedia