Overview of calculus
In this lesson, we'll give a broad overview and description of single-variable calculus. Single-variable calculus is a big tool kit for finding the slope or area underneath any arbitrary function \(f(x)\) which is smooth and continuous. If the slope of \(f(x)\) is constant, then we don't need calculus to find the slope or area; but when the slope of \(f(x)\) is a variable, then we must use a tool called a derivative to find the slope and another tool called an integral to find the area.
Limits
Limits describe what one quantity approaches as some other quantity approaches a given value. This concept is the basis of calculus because it is used to define both derivatives and integrals. In this lesson, we'll try to wrap our minds around what the notion of a limit is and use it to define the derivative function.
In this lesson, we’ll prove that \(\lim_{ϴ→0}\frac{sinϴ}{ϴ}=1\). We'll prove this result by using the squeeze theorem and basic geometry, algebra, and trigonometry. In a future lesson, we'll learn why this result is important: the reason being because knowledge that \(\lim_{ϴ→0}\frac{sinϴ}{ϴ}=1\) is required to find the derivatives of the sin and cosine functions. But we'll save that for a future lesson.
Derivatives
Limits describe what one quantity approaches as some other quantity approaches a given value. This concept is the basis of calculus because it is used to define both derivatives and integrals. In this lesson, we'll try to wrap our minds around what the notion of a limit is and use it to define the derivative function.
In previous lessons, we learned how the derivative \(f'(x)\) gives us the steepness at each point along a function \(f(x)\). In this lesson, we'll discuss how using the concept of a partial derivative we can find the steepness at each point along a surface \(z=f(x,y)\). To find the partial derivative we treat one of the variables as a constant and then take the ordinary derivative of \(f(x,y)\). Using this concept, we can specify how steep a surface \(f(x,y)\) is along the \(x\) direction and along the \(y\) direction at each point along the surface. In other words, for every point along the surface, there is a steepness of the surface associated with both the \(x\) and the \(y\) directions at that point.
Optimization problems
Calculus—specifically, derivatives—can be used to find the values of \(x\) at which the function \(f(x)\) is at either a minimum value or a maximum value. For example, suppose that we let \(x\) denote the horizontal distance away from the beginning of a hiking trail near a mountain and we let \(f(x)\) denote the altitude of the mountainous terrain at each \(x\) value. \(f(x)\) reaches a minimum value when the function "flattens out"—that is, when \(f'(x)\) becomes equal to zero. These particular values of \(x\) are associated with the bottom and top of the mountain. The condition that \(f'(x)=0\) only tells us that \(f(x)\) is at either a minimum or a maximum. To determine whether or not \(f(x)\) is at a minimum or a maximum, we must use the concept of the second derivative. This will be the topic of discussion in this lesson.
Given that the perimeter \(2x+2y\) of any arbitrary rectangle must be constant, we can use calculus to find that particular rectangle with the greatest area. The solution to this problem has practical applications. For example, suppose that someone had only 30 meters of fencing to enclose their backyard and they wanted to know what fencing layout would maximize the size and total area of their backyard. Using calculus, we can answer such questions.
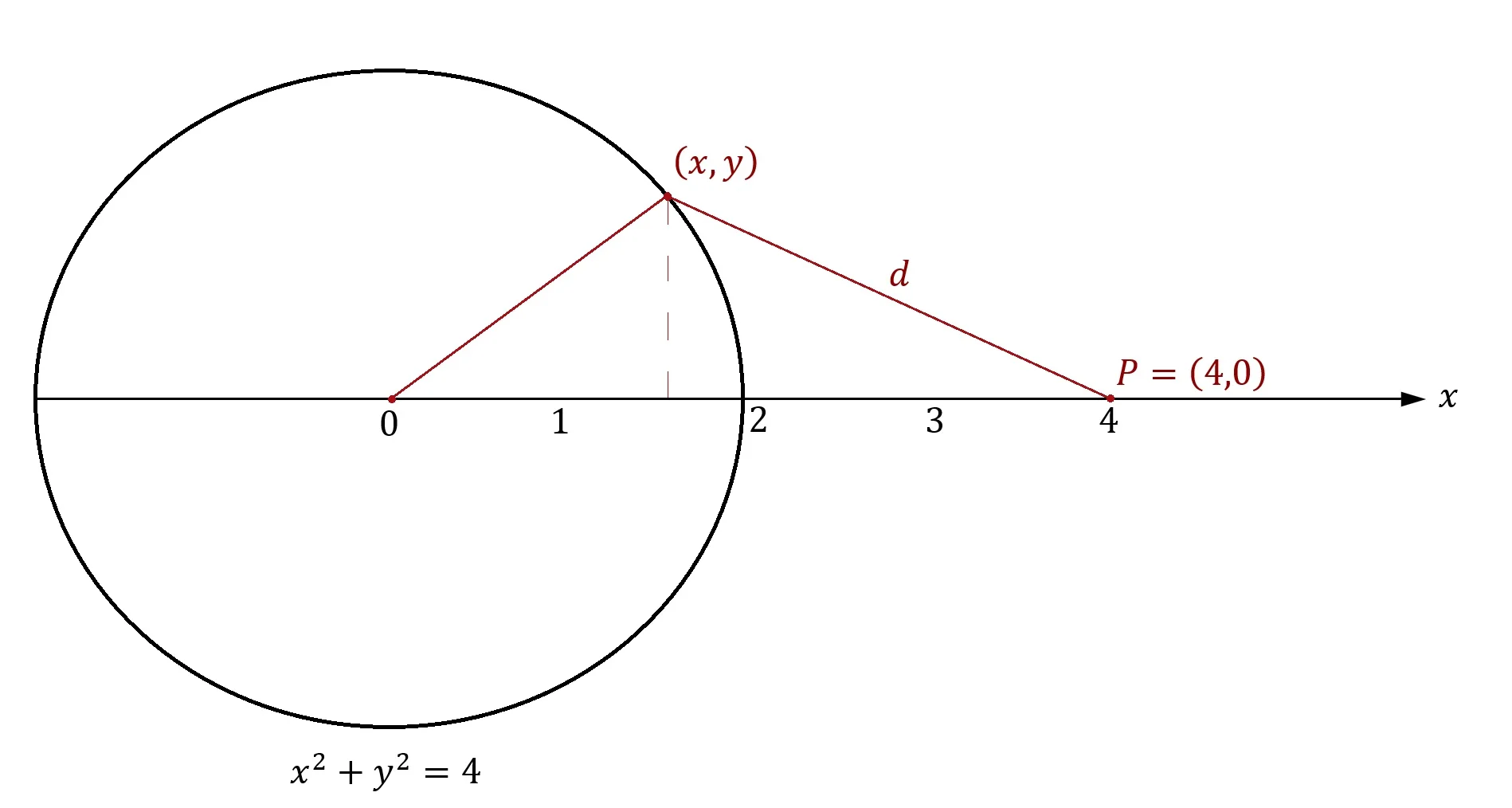
If \((x,y)\) represents any point on the circle, if \(P\) is a point fixed at the coordinate point \((4,0)\), and if \(d\) represents the distance between those two points then, by using only calculus, we can find the point \((x,y)\) on the circle associated with the minimum distance \(d\).
The law of reflection had been well known as early as the first century; but it took longer than another millennium to discover Snell's law, the law of refraction. The law of reflection was readily observable and could be easily determined by making measurements; this law states that if a light ray strikes a surface at an angle \(θ_i\) relative to the normal and gets reflected off of the surface, it will be reflected at an angle \(θ_r\) relative to the normal such that \(θ_i=θ_r\). The law of refraction, however, is a little less obvious and it required calculus to prove. The mathematician Pierre de Fermat postulated the principle of least time: that light travels along the path which gets it from one place to another such that the time \(t\) required to traverse that path is shorter than the time required to take any other path. In this lesson, we shall use this principle to derive Snell's law.
Chain rule
If water is being poured into a cone at a constant rate, what is the rate-of-change of the height of the water inside of the cone with respect to time? To answer this question, we'll need to use the chain rule.
Integrals
In this lesson, we define an integral as the Riemann sum as the number of rectangles approaches infinity.
In this lesson, we'll find the integral of any arbitrary function \(kx^n\) where \(k\) and \(n\) are any finite numbers such that \(n≠-1\).
In this lesson, we'll use the concept of a definite integral to calculate the arc length of a curve.
Using Newton's law of gravity and the concept of the definite integral, we can find the total gravitational force exerted by a rod on a particle a horizontal distance \(d\) away from the rod.
To find the gravitational force exerted by a disk on a particle a height \(h\) above the center of the disk, we must use Newton's law of gravity and the concept of a definite integral.
To find the gravitational force exerted by a sphere on a particle of mass \(M\) outside of that sphere, we must first subdivide that sphere into many very skinny shells and find the gravitational force exerted by anyone of those shells on \(m\). We'll see, however, that finding the gravitational force exerted by such a shell is in of itself a somewhat tedious exercise. In the end, we'll see that the gravitational force exerted by a sphere of mass \(M\) on a particle of mass \(m\) outside of the sphere (where \(D\) is the center-to-center separation distance between the sphere and particle) is completely identical to the gravitational force exerted by a particle of mass \(M\) on the mass \(m\) such that \(D\) is their separation distance.
In previous lessons, we learned that by taking the integral of some function \(f(x)\) we can find the area underneath that curve by summing the areas of infinitely many, infinitesimally skinny rectangles. In this lesson, we'll use the concept of a double integral to find the volume underneath any smooth and continuous surface \(f(x,y)\) by summing the volumes of infinitely many, infinitesimally skinny columns.
Line integrals are used to find the area between a surface \(f(x,y)\) and any arbitrary curve. In this lesson, we'll define the idea of line integral and derive a formula for calculating them.
In the previous lesson, we defined the concept of a line integral and derived a formula for calculating them. We learned that line integrals give the volume between a surface \(f(x,y)\) and a curve \(C\). In this lesson, we'll learn about some of the applications of line integral for finding the volumes of solids and calculating work. In particular, we'll use the concept of line integrals to calculate the volume of a cylinder, the work done by a proton on another proton moving in the presence of its electric field, and the work done by gravity on a swinging pendulum.
For a vector field \(\vec{F}(x,y)\) defined at each point \((x,y)\) within the region \(R\) and along the continuous, smooth, closed, piece-wise curve \(c\) such that \(R\) is the region enclosed by \(c\), we shall derive a formula (known as Green’s Theorem) which will allow us to calculate the line integral of \(\vec{F}(x,y)\) over the curve \(c\).
Solids of revolution
In this lesson, we'll use the concept of a definite integral to calculate the volume of a sphere. First, we'll find the volume of a hemisphere by taking the infinite sum of infinitesimally skinny cylinders enclosed inside of the hemisphere. Then we'll multiply our answer by two and we'll be done.
In this lesson, we'll discuss how by using the concept of a definite integral one can calculate the volume of something called an oblate spheroid. An oblate spheroid is essentially just a sphere which is compressed or stretched along one of its dimensions while leaving its other two dimensions unchanged. For example, the Earth is technically not a sphere—it is an oblate spheroid. To find the volume of an oblate spheroid, we'll start out by finding the volume of a paraboloid . (If you cut an oblate spheroid in half, the two left over pieces would be paraboloids.) To do this, we'll draw an \(n\) number of cylindrical shells inside of the paraboloid; by taking the Riemann sum of the volume of each cylindrical shell, we can obtain an estimate of the volume enclosed inside of the paraboloid. If we then take the limit of this sum as the number of cylindrical shells approaches infinity and their volumes approach zero, we'll obtain a definite integral which gives the exact volume inside of the paraboloid. After computing this definite integral, we'll multiply the result by two to get the volume of the oblate spheroid.
Series
In this article, we discuss various different ways to test whether or not a p-series diverges or converges.























In this lesson, we'll derive Maclaurin/Taylor polynomials which are used to "approximate" arbitrary functions which are smooth and continuous. More generally, they are used to give a local approximation of such functions. We'll also derive Maclaurin/Taylor series where the approximation becomes exact.